题目内容

函数f（x）=1-2|x|的图象大致是（　　）
A、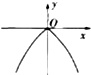
B、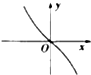
C、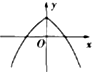
D、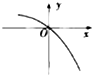
考点：函数的图象
专题：函数的性质及应用
分析：根据指数函数的图象和性质，求出函数f（x）的值域，问题得以解决
解答： 解：因为|x|≥0，
所以2|x|≥1，
所以f（x）=1-2|x|≤0恒成立，
故选：A
点评：本题考查了图象和识别，求出函数值域时常用的方法，属于基础题
练习册系列答案
相关题目
已知点（x0，y0）不在曲线f（x，y）=0上，曲线f（x，y）+af（x0，y0）=0（a∈R，且a≠0）与曲线f（x，y）=0的交点有（　　）
A、0个B、1个C、2个D、无数个
下列命题：
①?x∈R，x2+2＞0；
②?x∈N，x4≥1；
③?x∈Z，x2＜1；
④?x∈Q，x2=3．
其中正确命题的个数为（　　）
A、1B、2C、3D、4
求函数y=-2tan（3x+
π
3
）的定义域、值域，并指出它的周期、奇偶性和单调性．
若不等式ax2+8ax+21＜0的解集是{x|-7＜x＜-1}，那么a的值是（　　）
A、1B、2C、3D、4
已知实数x，y满足x-y+1=0（-1≤x≤4），则（x-3）2+y2的取值范围是
 
；
y-2
x
的取值范围是
 
．
已知等比数列{an}的公比q=3，前3项和S3=
13
3
．若函数f（x）=Asin（2x+φ）（A＞0，0＜φ＜π）在x=
π
6
处取得最大值，且最大值为a3．
（1）求函数f（x）的解析式．
（2）若f（
α
2
）=1，α∈（
π
2
，π），求sin（a+
π
2
）的值．
已知函数f（x）=
log2(x+3)，x≤-1
x2，-1＜x＜1
2x-1，x≥1

（1）求f（
2
-3）+f（-
3
2
）-f（-
21
8
）+f（
2
2
）+f（log23）的值；
（2）画出函数f（x）的图象，根据图象指出f（x）在区间[-2，3]上的单调区间及值域．
已知实数x，y满足
2x-y-2≤0
x-2y+2≥0
x+y+2≥0
，则z=-3x+2y的最大值为（　　）
A、-4B、2C、4D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网