题目内容
17．已知函数$f（x）=\left\{{\begin{array}{l}{2，x＞m}\\{{x^2}+4x+4，x≤m}\end{array}}\right.$的图象与直线y=x恰有三个公共点，则实数m的取值范围是（ ）| A． | （-∞，-1] | B． | [2，+∞） | C． | [-1，2] | D． | [-1，2） |
分析 由题意可得只要满足直线y=x和射线y=2（x＞m）有一个交点，而且直线y=x与函数f（x）=x2+4x+2的两个交点即可，画图便知，直线y=x与函数f（x）=x2+4x+2的图象的两个交点为（-2，-2）（-1，-1），由此可得实数m的取值范围．
解答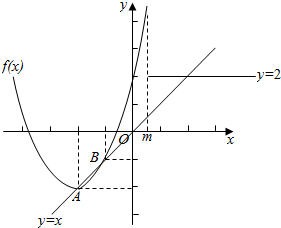 
解：由题意可得射线y=x与函数f（x）=2（x＞m）有且只有一个交点．
而直线y=x与函数f（x）=x2+4x+2，至多两个交点，
题目需要三个交点，则只要满足直线y=x与函数f（x）=x2+4x+2的图象有两个交点即可，
画图便知，y=x与函数f（x）=x2+4x+2的图象交点为A（-2，-2）、B（-1，-1），
故有 m≥-1．
而当m≥2时，直线y=x和射线y=2（x＞m）无交点，故实数m的取值范围是[-1，2），
故选：D．
点评 本题主要考查函数与方程的综合应用，体现了转化、数形结合的数学思想，属于中档题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
7．已知y=f′（x）是函数$f（x）=\frac{1}{3}{x^3}+2{x^2}+5$的导数，则f′（1）=（ ）
| A． | $\frac{22}{3}$ | B． | 10 | C． | 5 | D． | $\frac{10}{9}$ |
8．在研究色盲与性别的关系调查中，调查了男性240人，其中有40人患色盲，调查的260名女性中有10人患色盲．
（Ⅰ）根据以上数据建立一个2×2列联表；
（Ⅱ）能否有99.9%的把握认为“性别与患色盲有关系”？
附1：随机变量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
附2：临界值参考表：
（Ⅰ）根据以上数据建立一个2×2列联表；
（Ⅱ）能否有99.9%的把握认为“性别与患色盲有关系”？
附1：随机变量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
附2：临界值参考表：
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5．设命题P：?x∈R，ex＞1，则￢P为（ ）
| A． | ?x∈R，ex=1 | B． | ?x∈R，ex＞1 | C． | ?x∈R，ex≤1 | D． | ?x∈R，ex≤1 |
2．对抛物线y=4x2，下列描述正确的是（ ）
| A． | 开口向右，焦点为（1，0） | B． | 开口向上，焦点为（0，1） | ||
| C． | 开口向上，焦点为（0，$\frac{1}{16}$） | D． | 开口向右，焦点为（$\frac{1}{16}$，0） |
6．在△ABC中，角A，B，C的对边分别为a，b，c，已知C=120°，b=1，S△ABC=$\sqrt{3}$，则c=（ ）
| A． | $\sqrt{21}$ | B． | $\sqrt{13}$ | C． | 4 | D． | 3 |