题目内容
12.已知f(x)=ex,g(x)=x+1.(1)证明:f(x)≥g(x);
(2)求y=f(x),y=g(x)与x=-1所围成的封闭图形的面积.
分析 (1)设h(x)=f(x)-g(x),则h′(x)=ex-1 h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,即可证明结论;
(2)利用S=${∫}_{-1}^{0}({e}^{x}-x-1)dx$,即可得出结论.
解答 (1)证明:设h(x)=f(x)-g(x),则h′(x)=ex-1
∴h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴h(x)≥h(0)=0,
∴f(x)≥g(x);
(2)解:S=${∫}_{-1}^{0}({e}^{x}-x-1)dx$=$({e}^{x}-\frac{1}{2}{x}^{2}-x){|}_{-1}^{0}$=$\frac{1}{2}-\frac{1}{e}$.
点评 本题考查不等式的证明,考查定积分知识的运用,属于中档题.

练习册系列答案
相关题目
17.已知函数$f(x)=\left\{{\begin{array}{l}{2,x>m}\\{{x^2}+4x+4,x≤m}\end{array}}\right.$的图象与直线y=x恰有三个公共点,则实数m的取值范围是( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | [-1,2] | D. | [-1,2) |
4.命题P:“A>30°”是命题Q:“sinA>$\frac{1}{2}$”的( )条件.
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
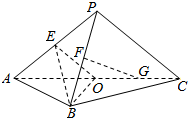 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.