题目内容
14.已知函数$f(x)=\frac{{{e^{2x}}-{e^x}sinx+1}}{{{e^{2x}}+1}}$的最大值为M,最小值为m,则M+m的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 由f(x)=1+$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,令g(x)=$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,x∈R,判断g(x)为奇函数,其最值之和为0,即可得到所求和.
解答 解:函数$f(x)=\frac{{{e^{2x}}-{e^x}sinx+1}}{{{e^{2x}}+1}}$
=1+$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,
令g(x)=$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,x∈R,
则g(-x)=$\frac{{e}^{-x}sin(-x)}{1+{e}^{-2x}}$=$\frac{{e}^{x}(-sinx)}{{e}^{2x}+1}$=-g(x),
可得g(x)为奇函数,
由奇函数的图象关于原点对称,可得g(x)的最大值A和最小值a之和为0,
则M+m=(A+1)+(a+1)=(A+a)+2=2.
故选:C.
点评 本题考查函数的最值的求法,注意运用转化思想和构造函数法,运用奇函数的图象关于原点对称,其最值之和为0是解题的关键,属于中档题.

练习册系列答案
相关题目
4.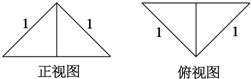 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
2.执行下面的程度框图,若输出的值为-5,则判断框中可以填( )


| A. | z>10 | B. | z≤10 | C. | z>20 | D. | z≤20 |
9.下列程序:

输出的结果a是( )

输出的结果a是( )
| A. | 120 | B. | 15 | C. | 6 | D. | 5 |
19.已知集合A={x∈R|x>$\sqrt{π}$),π为圆周率,则( )
| A. | 2∈A | B. | 2∉A | C. | 2>A | D. | 2?A |
6.如果a>b>0,那么下列不等式中不正确的是( )
| A. | ab>b2 | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | a2>ab |
3.高三学生小罗利用暑假参加社会实践,为了帮助贸易公司的购物网站优化今年国庆节期间的营销策略,他对去年10月1日当天在该网站消费且消费金额不超过1000元的1000名(女性800名,男性200名)网购者,根据性别按分层抽样的方法抽取100名进行分析,得到如下统计图表(消费金额单位:元):
女性消费情况:
男性消费情况:
(Ⅰ)现从抽取的100名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的这两名网购者恰好是一男一女的概率;
(Ⅱ)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写右面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
附:
(${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 5 | 10 | 15 | 47 | x |
男性消费情况:
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 2 | 3 | 10 | y | 2 |
(Ⅱ)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写右面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
4.如果a,b是异面直线,那么和a,b都垂直的直线( )
| A. | 有且只有一条 | B. | 有一条或两条 | C. | 不存在或一条 | D. | 有无数多条 |