题目内容
满足性质f(x+y)=f(x)+f(y)的函数是( )
| A、f(x)=3x |
| B、f(x)=3x+1 |
| C、f(x)=x2 |
| D、f(x)=3|x| |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:可通过一一加以判断f(x+y)=f(x)+f(y)是否成立,即可得到答案.
解答:
解:对于A.f(x+y)=3(x+y)=3x+3y=f(x)+f(y),成立;
对于B.f(x+y)=3(x+y)+1,f(x)+f(y)=3x+3y+2,不成立;
对于C.f(x+y)=(x+y)2,f(x)+f(y)=x2+y2,不成立;
对于D.f(x+y)=3|x+y|,f(x)+f(y)=3|x|+3|y|,不成立.
故选:A.
对于B.f(x+y)=3(x+y)+1,f(x)+f(y)=3x+3y+2,不成立;
对于C.f(x+y)=(x+y)2,f(x)+f(y)=x2+y2,不成立;
对于D.f(x+y)=3|x+y|,f(x)+f(y)=3|x|+3|y|,不成立.
故选:A.
点评:本题考查抽象函数及运用,考查函数的具体模型,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={y|y=2x},B={y|y=log2x},则A与B的关系是( )
| A、A=B | B、A∩B=∅ |
| C、A?B | D、A⊆B |
一个简单几何体的正视图、俯视图如图所示,则其侧视图不可能是( )
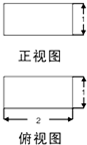

| A、正方形 | B、直角梯形 |
| C、等腰三角形 | D、圆 |
设集合M={x|x>1},N={x|x2>1},则下列关系中正确的是( )
| A、M=N | B、M∪N=N |
| C、M∪N=M | D、M∩N=N |
若M点的极坐标为(-2,-
),则M点的直角坐标是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
下列命题是假命题的是( )
A、已知向量
| ||||||||
B、函数y=x(2
| ||||||||
C、直线x+
| ||||||||
D、关于x的方程2sin(x-
|