题目内容
对于区间[a,b]上有意义的两个函数f(x)与g(x),如果对于区间[a,b]中的任意数x均有|f(x)-g(x)|≤1,则称函数f(x)与g(x)在区间[a,b]上是密切函数,[a,b]称为密切区间.若m(x)=x2-3x+4与n(x)=2x-3在某个区间上是“密切函数”,则它的一个密切区间可能是( )
| A、[3,4] |
| B、[2,4] |
| C、[1,4] |
| D、[2,3] |
考点:函数的值域,函数的定义域及其求法
专题:新定义,函数的性质及应用
分析:本题可以先将解不等式-1≤f(x)-g(x)≤1,得到一个解集,再从选项中找出解集的一个子集(闭区间),即得本题答案.
解答:
解:∵m(x)=x2-3x+4与n(x)=2x-3,
∴m(x)-n(x)=(x2-3x+4)-(2x-3)=x2-5x+7.
令-1≤x2-5x+7≤1,
则有
,
∴2≤x≤3.
故答案为D.
∴m(x)-n(x)=(x2-3x+4)-(2x-3)=x2-5x+7.
令-1≤x2-5x+7≤1,
则有
|
∴2≤x≤3.
故答案为D.
点评:本题考查了新定义函数和解一元二次不等式组,本题的计算量不大,新定义也比较容易理解,属于基础题.

练习册系列答案
相关题目
参数方程
(θ为参数)化为普通方程是( )
|
| A、(x-1)2+(y+3)2=1 |
| B、(x+3)2+(y-1)2=4 |
| C、(x-2)2+(y+2)2=4 |
| D、x+y-2=0 |
若在三角形ABC中,已知a2=b2+c2+bc,则角A为( )
| A、60° | B、120° |
| C、30° | D、60°或120° |
已知椭圆O:
+
=1的离心率为e1,动△ABC是其内接三角形,且
=
+
.若AB的中点为D,D的轨迹E的离心率为e2,则( )
| x2 |
| a2 |
| y2 |
| b2 |
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| A、e1=e2 |
| B、e1<e2 |
| C、e1>e2 |
| D、e1e2=1 |
函数f(x)=
x2-lnx的单调递减区间为( )
| 1 |
| 2 |
| A、(-1,1) |
| B、(0,1] |
| C、[1,+∞) |
| D、(-∞,-1)∪(0,1] |
在空间直坐标系中,点P在x轴上,它到P1(0,
,3)的距离为2
,则点P的坐标为( )
| 2 |
| 3 |
| A、(0,1,0)或(0,-1,0) |
| B、(1,0,0) |
| C、(1,0,0)或(-1,0,0) |
| D、(0,1,0)或(0,0,1) |
若抛物线y2=2px的焦点与椭圆
+
=1的右焦点重合,则p的值为( )
| x2 |
| 8 |
| y2 |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
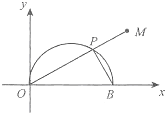 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度. 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,