题目内容
 如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
| ||
| 4 |
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:由题设条件推导出△ABE∽△ADC,从而得到AB•AC=AD•AE,再由S=
AB•ACsin∠BAC,且S=
AD•AE,能求出sin∠BAC=
,由此能求出∠BAC.
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
解答:
解:∵△ABC的角平分线AD的延长线交它的外接圆于E,
∴∠BAE=∠CAD,
∵∠AEB与∠ACB是同弧上的圆周角,
∴∠AEB=∠ACD,
∴△ABE∽△ADC,∴
=
,即AB•AC=AD•AE,
∵S=
AB•ACsin∠BAC,且S=
AD•AE,
∴sin∠BAC=
,
又∵∠BAC是三角形内角,
∴∠BAC=60°.
∴∠BAE=∠CAD,
∵∠AEB与∠ACB是同弧上的圆周角,
∴∠AEB=∠ACD,
∴△ABE∽△ADC,∴
| AB |
| AE |
| AD |
| AC |
∵S=
| 1 |
| 2 |
| ||
| 4 |
∴sin∠BAC=
| ||
| 2 |
又∵∠BAC是三角形内角,
∴∠BAC=60°.
点评:本题考查角的大小的求法,是中档题,解题时要注意圆的性质和三角形面积公式的合理运用.

练习册系列答案
相关题目
 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,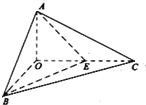 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.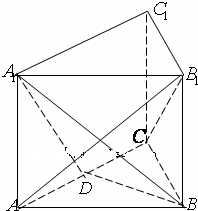 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为