题目内容
已知命题p：函数y=logm（6-mx）在[1，2]上单调递减．
（1）求实数m的取值范围；
（2）命题q：方程x2-2x+m+1=0在（0，+∞）内有一个根．若p或q为真，p且q为假，求实数m的取值范围．
（1）求实数m的取值范围；
（2）命题q：方程x2-2x+m+1=0在（0，+∞）内有一个根．若p或q为真，p且q为假，求实数m的取值范围．
考点：复合命题的真假
专题：函数的性质及应用,简易逻辑
分析：对于（1），根据复合函数性质求即可；对于（2），先求出p与q，再根据“p或q为真，p且q为假”
得到p、q一真一假，然后取并集运算．
得到p、q一真一假，然后取并集运算．
解答：
解：（1）
，∴1＜m＜3
（2）f（x）对称轴为x=1，
①当△=4-4（m+1）=0时，m=0，f（x）=0的根为1，符合题意；
②当△＞0即m＜0时，f（0）=m+1≤0，∴m≤-1
综上，m的取值范围是（-∞，-1]∪{0}．
由p、q一真一假，得
或
，
∴m∈（-∞，-1]∪{0}∪（1，3）
|
（2）f（x）对称轴为x=1，
①当△=4-4（m+1）=0时，m=0，f（x）=0的根为1，符合题意；
②当△＞0即m＜0时，f（0）=m+1≤0，∴m≤-1
综上，m的取值范围是（-∞，-1]∪{0}．
由p、q一真一假，得
|
|
∴m∈（-∞，-1]∪{0}∪（1，3）
点评：本题考查了复合函数的单调性，方程的根，以及逻辑推理，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
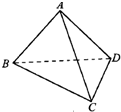如图四面体ABCD的棱BD长为2，其余各棱长均为
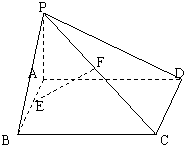如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点．
在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”，所有“折线路径”中长度最小的称为M到N的“折线距离”．如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”．某地有三个居民区分别位于平面xOy内三点A（-8，1），B（5，2），C（1，14），现计划在这个平面上某一点P（x，y）处修建一个超市．