题目内容
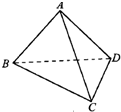 如图四面体ABCD的棱BD长为2,其余各棱长均为
如图四面体ABCD的棱BD长为2,其余各棱长均为| 2 |
考点:二面角的平面角及求法
专题:计算题,空间角
分析:取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,得∠AEC就是A-BD-C的二面角,解三角形ACE即可得到二面角A-BD-C的大小.
解答:
 解:取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,
解:取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,
∴∠AEC是二面角A-BD-C的平面角.
∵四面体ABCD的棱BD长为2,其余各棱长均为
,
∴AE=1,CE=1,AC=
,
∴AE2+CE2=AC2,
∴AE⊥EC,
∴二面角A-BD-C的大小为90°.
 解:取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,
解:取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,∴∠AEC是二面角A-BD-C的平面角.
∵四面体ABCD的棱BD长为2,其余各棱长均为
| 2 |
∴AE=1,CE=1,AC=
| 2 |
∴AE2+CE2=AC2,
∴AE⊥EC,
∴二面角A-BD-C的大小为90°.
点评:本题考查的知识点是二面角的平面角及求法,其中构造出二面角A-BD-C的平面角∠AEC是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数1-2i(i是虚数单位)的虚部是( )
| A、2i | B、-2i | C、2 | D、-2 |
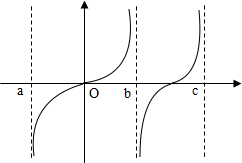 已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断:
已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断: