题目内容
7.已知数列{an}满足a1=1,an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1(n≥2,n∈N+),则a2016=1008.分析 利用递推关系可得an+1-an=$\frac{1}{n}{a}_{n}$,化为:$\frac{{a}_{n+1}}{n+1}=\frac{{a}_{n}}{n}$=…=$\frac{{a}_{2}}{2}$=$\frac{1}{2}$,即可得出.
解答 解:∵数列{an}满足a1=1,an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1(n≥2,n∈N+),
∴a2=a1=1,an+1=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1+$\frac{1}{n}{a}_{n}$,
∴an+1-an=$\frac{1}{n}{a}_{n}$,
化为:$\frac{{a}_{n+1}}{n+1}=\frac{{a}_{n}}{n}$=…=$\frac{{a}_{2}}{2}$=$\frac{1}{2}$,
∴an=$\frac{n}{2}$.(n≥2)
则a2016=$\frac{2016}{2}$=1008.
故答案为:1008.
点评 本题考查了递推关系的应用、数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
18.已知圆C:x2+y2=9,直线l1:x-y-1=0与l2:x+2y-10=0的交点设为P点,过点P向圆C作两条切线a,b分别与圆相切于A,B两点,则S△ABP=$\frac{192}{25}$.
19.如果二次函数y=x2+4x+(m+3)有两个不同的零点,则m的取值范围是( )
| A. | (-∞,1) | B. | (-2,6) | C. | [-2,6] | D. | {-2,6} |
16.函数$f(x)=\left\{\begin{array}{l}2x-{x^2},0≤x≤3\\{x^2}+6x,-2≤x<0\end{array}\right.$的值域是( )
| A. | [-8,1] | B. | [-8,-3] | C. | R | D. | [-9,1] |
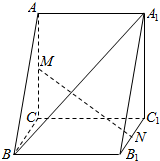 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.