题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{{x}^{2}+4x+1,x≤0}\end{array}\right.$,(1)求函数f(x)的零点;
(2)g(x)=f(x)-a 若函数g(x)有四个零点,求a的取值范围;
(3)在(2)的条件下,记g(x)得四个零点从左到右分别为x1,x2,x3,x4,求x1+x2+x3x4值.
分析 (1)讨论当x>0时,当x≤0时,由f(x)=0,解方程即可得到零点;
(2)由题意可得f(x)=a有四个不等实根,画出函数y=f(x)的图象,通过图象观察,即可得到a的范围;
(3)由二次函数的对称性和对数的运算性质,结合图象即可得到所求和.
解答 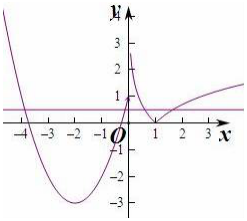 解:(1)函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{{x}^{2}+4x+1,x≤0}\end{array}\right.$,
解:(1)函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{{x}^{2}+4x+1,x≤0}\end{array}\right.$,
当x>0时,由|lnx|=0解得x=1,
当x≤0时,由x2+4x+1=0解得x=-2+$\sqrt{3}$或x=-2-$\sqrt{3}$,
可得函数的零点为1,-2+$\sqrt{3}$或-2-$\sqrt{3}$;
(2)g(x)=f(x)-a 若函数g(x)有四个零点,
即为f(x)=a有四个不等实根,画出函数y=f(x)的图象,
由图象可得当0<a≤1时,f(x)的图象和直线y=a有四个交点,
故函数g(x)有四个零点时a的取值范围是0<a≤1;
(3)由y=x2+4x+1的对称轴为x=-2,
可得x1+x2=-4,
由|lnx3|=|lnx4|=a,
即-lnx3=lnx4,即为lnx3+lnx4=0
则x3x4=1,
故x1+x2+x3x4=-3.
点评 本题考查函数的零点问题的解法,注意运用转化思想和数形结合思想,考查对数的运算性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.命题“对任意的x∈R,x3-x+1≤0”的否定是( )
| A. | 不存在x∈R,x3-x+1≤0 | B. | 存在x∈R,x3-x+1≤0 | ||
| C. | 对任意的x∈R,x3-x+1>0 | D. | 存在x∈R,x3-x+1>0 |
10.设$f(x)=\left\{\begin{array}{l}x+4,x≤-2或x≥3\\{x^2}-1,-2<x<3\end{array}\right.$,若函数y=f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是( )
| A. | (-2,1) | B. | [0,1] | C. | [-2,0) | D. | [-2,1) |