题目内容
2.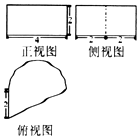 已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )| A. | 4π+8 | B. | 4π+12 | C. | 8π+8 | D. | 8π+12 |
分析 由已知中的三视图,可得该几何体是一个以俯视图为底面的柱体,代入柱体体积公式,可得答案.
解答 解:由已知中的三视图,可得该几何体是一个以俯视图为底面的柱体,
(也可看成是一个三棱柱和半圆柱的组合体),
其底面面积S=$\frac{1}{2}$×2×4+$\frac{1}{2}$π•22=2π+4,
高h=2,
故几何体的体积V=Sh=4π+8,
故选:A
点评 本题考查的知识点是圆柱的体积和表面积,棱柱的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
10.若存在实数α∈R,$β∈[\frac{π}{2},π]$,使得实数t同时满足$t={cos^2}β+\frac{α}{2}cosβ$,α≤t≤α-2cosβ,则t的取值范围是( )
| A. | $[-\frac{2}{3},0]$ | B. | $[0,\frac{4}{3}]$ | C. | $[\frac{4}{3},2]$ | D. | [2,4] |
11.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=-4x+3sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
12.已知直线l:$\sqrt{3}x-y+4=0$与圆x2+y2=16交于A,B两点,则$\overrightarrow{AB}$在x轴正方向上投影的绝对值为( )
| A. | $4\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
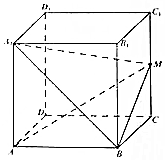 已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.
已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.