题目内容
已知函数f(x)=
.
(Ⅰ)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;
(Ⅱ)求该函数在区间[1,5]上的最大值和最小值.
| 3x+1 |
| x+2 |
(Ⅰ)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;
(Ⅱ)求该函数在区间[1,5]上的最大值和最小值.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ)可将原函数变成f(x)=3-
,根据单调性的定义,通过该函数解析式即可判断函数f(x)在[1,+∞)上为增函数.可利用求函数导数,判断导数符号的方法来证明该结论;
(Ⅱ)由(Ⅰ)即知f(x)在[1,5]上单调递增,所以最大值f(5),最小值f(1).
| 5 |
| x+1 |
(Ⅱ)由(Ⅰ)即知f(x)在[1,5]上单调递增,所以最大值f(5),最小值f(1).
解答:
解:(Ⅰ)f(x)在[1,+∞)上是增函数,证明:f′(x)=
>0;
∴f(x)在[1,+∞)上为增函数;
(Ⅱ) 由(Ⅰ)知f(x)在[1,5]上单调递增;
∴此时,f(x)的最大值为f(5)=
,最小值为f(1)=
.
| 5 |
| (x+2)2 |
∴f(x)在[1,+∞)上为增函数;
(Ⅱ) 由(Ⅰ)知f(x)在[1,5]上单调递增;
∴此时,f(x)的最大值为f(5)=
| 16 |
| 7 |
| 4 |
| 3 |
点评:考察通过解析式的形式及单调性的定义判断函数单调性的方法,以及利用导数证明函数单调性的方法,以及根据函数单调性求函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
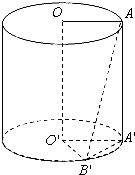 圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求:
圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求: