题目内容
已知sin( α+
)=
,且α∈(0,π),则tanα= .
| π |
| 6 |
| 1 |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由sin( α+
)=
,且α∈(0,π),可得cos( α+
)=-
,利用两角差的正弦和余弦公式,可得sinα=
,cosα=
.进而根据tanα=
可得答案.
| π |
| 6 |
| 1 |
| 3 |
| π |
| 6 |
2
| ||
| 3 |
| ||||
| 6 |
-3
| ||
| 6 |
| sinα |
| cosα |
解答:
解:∵sin( α+
)=
,且α∈(0,π),
∴sinα>0,
则cos( α+
)=±
=±
,
若cos( α+
)=
,
则sinα=sin[( α+
)-
]=
•
-
×
<0,不满足条件;
若cos( α+
)=-
,
则sinα=sin[( α+
)-
]=
•
+
×
=
,
cosα=cos[( α+
)-
]=-
•
+
•×
=
.
故tanα=
=
=-
,
故答案为:
| π |
| 6 |
| 1 |
| 3 |
∴sinα>0,
则cos( α+
| π |
| 6 |
1-sin2(α+
|
2
| ||
| 3 |
若cos( α+
| π |
| 6 |
2
| ||
| 3 |
则sinα=sin[( α+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
若cos( α+
| π |
| 6 |
2
| ||
| 3 |
则sinα=sin[( α+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
| ||||
| 6 |
cosα=cos[( α+
| π |
| 6 |
| π |
| 6 |
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
-3
| ||
| 6 |
故tanα=
| sinα |
| cosα |
| ||||||
|
5
| ||||
| 53 |
故答案为:
5
| ||||
| 53 |
点评:本题考查的知识点是两角和与差的正弦函数和余弦函数,同角三角函数的基本关系,解答时要注意α不可能为锐角.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,当a=3和a=5时,点P的轨迹分别为( )
| A、都是双曲线 |
| B、都是射线 |
| C、双曲线的一支和一条射线 |
| D、都是双曲线的一支 |
 如图,已知抛物线C:x2=4y,过焦点F任作一条直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛物线C:x2=4y,过焦点F任作一条直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).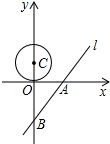 如图所示,已知直线l的解析式是y=
如图所示,已知直线l的解析式是y=