题目内容
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b,b>0)的渐近线方程为y=±x,且经过点$(\sqrt{2},1)$,则该双曲线的方程为x2-y2=1.分析 根据题意,设双曲线的方程为(x+y)(x-y)=λ(λ≠0),代入点$(\sqrt{2},1)$即可求出双曲线的方程.
解答 解:∵双曲线的渐近线方程为y=±x,
∴设双曲线的方程为(x+y)(x-y)=λ(λ≠0),
即x2-y2=λ,
∵双曲线过点$(\sqrt{2},1)$.∴2-1=λ,
∴λ=1,
∴x2-y2=1.
故答案为:x2-y2=1.
点评 本题主要考查了双曲线的标准方程.解题的关键是设双曲线的方程为(x+y)(x-y)=λ(λ≠0).

练习册系列答案
相关题目
7.已知等差数列{an}的前n项和为Sn,5a4+4a5=-22,S6=2a4-5
(1)求数列{an}的通项公式;
(2)设${b_n}={2^{{a_n}-2}}-n$,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设${b_n}={2^{{a_n}-2}}-n$,求数列{bn}的前n项和Tn.
11.设n=${∫}_{0}^{2}$3x2dx,则(x-$\frac{1}{2x}$)n的展开式中的常数项为( )
| A. | -$\frac{35}{8}$ | B. | $\frac{35}{8}$ | C. | -70 | D. | 70 |
6.某几何体的三视图细图所示,则该几何体的体积为( )
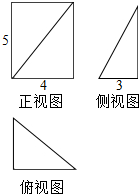

| A. | 12 | B. | 13 | C. | 18 | D. | 20 |