题目内容
11.设n=${∫}_{0}^{2}$3x2dx,则(x-$\frac{1}{2x}$)n的展开式中的常数项为( )| A. | -$\frac{35}{8}$ | B. | $\frac{35}{8}$ | C. | -70 | D. | 70 |
分析 利用定积分求出n,再求出展开式通项,令x的指数为0,即可求出展开式中的常数项.
解答 解:n=${∫}_{0}^{2}$3x2dx=x3|${\;}_{0}^{2}$=8,
(x-$\frac{1}{2x}$)n展开式的通项公式为Tk+1=Cnkxn-k•(-1)k(2x)-k=(-$\frac{1}{2}$)kCnkxn-2k,
当n-2k=0时,即8-2k=0时,k=4时,展开式为常数项,
∴T5=(-$\frac{1}{2}$)4C84=$\frac{35}{8}$.
故选:B.
点评 本题考查展开式中的常数项,考查二项式定理的应用,考查学生的计算能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.对抛物线y=4x2,下列描述正确的是( )
| A. | 开口向右,焦点为(1,0) | B. | 开口向上,焦点为(0,1) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |
19.关于直线2x-y=2与直线x+2y=1的关系,正确的说法是( )
| A. | 重合 | B. | 相交但不垂直 | C. | 垂直 | D. | 平行 |
6.在△ABC中,角A,B,C的对边分别为a,b,c,已知C=120°,b=1,S△ABC=$\sqrt{3}$,则c=( )
| A. | $\sqrt{21}$ | B. | $\sqrt{13}$ | C. | 4 | D. | 3 |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b,b>0)的渐近线方程为y=±x,且经过点$(\sqrt{2},1)$,则该双曲线的方程为x2-y2=1.
20.一梯形的直观图是一个如图所示的等腰梯形,且此梯形的面积为$\sqrt{2}$,则原梯形的面积为( )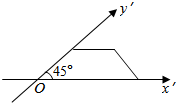

| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |