题目内容
8.等比数列{an}同时满足下列条件:a1+a6=33;a3a4=32.(1)求数列{an}的通项;
(2)若4a2,2a3,a4构成等差数列,求{an}的前6项和S6.
分析 (1)运用等比数列的通项公式,解方程可得首项和公比,即可得到所求通项;
(2)由等差数列的中项性质,结合等比数列的通项公式,解方程可得公比为2,再由等比数列的求和公式,即可得到所求和.
解答 解:(1)设等比数列{an}的公比为q,
由a3a4=a1a6,可得a1a6=32,a1+a6=33,
解得a1=1,a6=32;或a1=32,a6=1.
可得q5=32或q5=$\frac{1}{32}$,
解得q=2或q=$\frac{1}{2}$,
可得an=2n-1;或an=32•($\frac{1}{2}$)n-1;
(2)4a2,2a3,a4构成等差数列,
可得4a3=4a2+a4,
即有4a1q2=4a1q+a1q3,
即q2-4q+4=0,解得q=2,
即有an=2n-1;
则{an}的前6项和S6=$\frac{1-{2}^{6}}{1-2}$=63.
点评 本题考查等比数列的通项公式和求和公式的运用,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
19.关于直线2x-y=2与直线x+2y=1的关系,正确的说法是( )
| A. | 重合 | B. | 相交但不垂直 | C. | 垂直 | D. | 平行 |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b,b>0)的渐近线方程为y=±x,且经过点$(\sqrt{2},1)$,则该双曲线的方程为x2-y2=1.
20.一梯形的直观图是一个如图所示的等腰梯形,且此梯形的面积为$\sqrt{2}$,则原梯形的面积为( )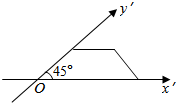

| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |