题目内容
已知C:(x-4)2+(y-3)2=25,过圆C内一定点P(2,1)作两条直线AC与BD,若弦AC与BD所成的夹角为90゜,求四边ABCD面积的最大值.
考点:直线与圆的位置关系
专题:直线与圆
分析:根据题意得到当过P点为直径与和直径垂直的两条弦时四边形ABCD面积最大,求出|CP|的距离,由勾股定理求出短弦长,利用直径与短弦乘积的一半即可求出面积的最大值.
解答:
 解:当BD为圆直径时,由BD⊥AC,得到P为AC的中点,
解:当BD为圆直径时,由BD⊥AC,得到P为AC的中点,
在Rt△ACP中,|CP|=
=2
,
根据勾股定理得:|AP|=
=
,即|AC|=2|AP|=2
,
则(S四边形ABCD)max=
AC•BD=
×2
×10=10
.
 解:当BD为圆直径时,由BD⊥AC,得到P为AC的中点,
解:当BD为圆直径时,由BD⊥AC,得到P为AC的中点,在Rt△ACP中,|CP|=
| (4-2)2+(3-1)2 |
| 2 |
根据勾股定理得:|AP|=
| |AC|2-|CP|2 |
| 17 |
| 17 |
则(S四边形ABCD)max=
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 17 |
点评:此题考查了直线与圆的位置关系,画出四边形ABCD面积最大值的图形是解本题的关键.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
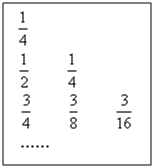 如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )
如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )A、
| ||
B、
| ||
C、
| ||
D、
|
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、log20.8<0.993.3<log3π |
| D、0.993.3<log20.8 l<log3π |
 如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.
如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.