题目内容
抛物线y2=8x的焦点与椭圆
+
=1的焦点重合,则椭圆的离心率为( )
| x 2 |
| a 2 |
| y 2 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点坐标,由椭圆的一个焦点与抛物线的焦点重合得到椭圆是焦点在x轴上的椭圆,且求得半焦距c,然后利用a2=b2+c2求出椭圆的半长轴,则离心率可求.
解答:
解:由题意可得:抛物线y2=8x的焦点(2,0),
∵抛物线y2=8x的焦点与椭圆
+
=1的焦点重合,
∴a2-5=4,∴a2=9,
解得:a=3.
∴e=
=
.
故选A.
∵抛物线y2=8x的焦点与椭圆
| x 2 |
| a 2 |
| y 2 |
| 5 |
∴a2-5=4,∴a2=9,
解得:a=3.
∴e=
| c |
| a |
| 2 |
| 3 |
故选A.
点评:本题考查了椭圆的简单性质,涉及圆锥曲线离心率的求解问题,一定要找到关于a,c的关系,隐含条件a2=b2+c2的应用是解答该题的关键,此题是基础题.

练习册系列答案
相关题目
不等式x2≥2x的解集是( )
| A、{x|x≥2} |
| B、{x|x≤2} |
| C、{x|0≤x≤2} |
| D、{x|x≤0或x≥2} |
已知正项非常值数列{an},{bn}满足:an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列.令cn=
,则下列关于数列{cn}的说法正确的是( )
| bn |
| A、该数列为等差数列 |
| B、该数列为等比数列 |
| C、该数列的每一项为奇数 |
| D、该数列的每一项为偶数 |
在三棱柱ABC-A1B1C1中,已知AA1⊥平面ABC,AA1=2,BC=2
,∠BAC=
,此三棱柱各个顶点都在一个球面上,则球的体积为( )
| 3 |
| π |
| 2 |
A、
| ||
| B、16π | ||
C、
| ||
D、
|
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
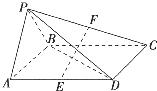 四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=