题目内容
7.函数f(x)=Asin(ωx+φ),x∈R(0,ω>0,0<φ<$\frac{π}{2}$)的图象与x轴的交点中,相邻两个交点之间的距离为$\frac{π}{2}$,且图象上一个最低点为M($\frac{2π}{3}$,-2).(1)求函数f(x)的解析式及单调增区间;
(2)求 当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时,f(x)的值域.
分析 (1)由最低点可求A,由已知可得周期T=π,利用周期公式可求ω,利用点$M({\frac{2π}{3},-2})$在图象上,结合范围$φ∈({0,\frac{π}{2}})$,可求φ,可求函数解析式,利用正弦函数的单调性可求单调递增区间.
(2)由$x∈[{\frac{π}{12},\frac{π}{2}}]$,可求范围$2x+\frac{π}{6}∈[{\frac{π}{3},\frac{7π}{6}}]$,利用正弦函数的图象和性质可求其值域.
解答 解:(1)∵依题意,由最低点为$M({\frac{2π}{3},-2})$,得A=2,
又∵周期T=π,∴ω=2.
∵由点$M({\frac{2π}{3},-2})$在图象上,
∴得$2sin({\frac{4π}{3}+φ})=-1$,
∴$\frac{4π}{3}+φ=-\frac{π}{2}+2kπ,k∈{Z}$,
∴$φ=-\frac{11π}{6}+2kπ$.
∵$φ∈({0,\frac{π}{2}})$,
∴$φ=\frac{π}{6}$,
∴$f(x)=2sin({2x+\frac{π}{6}})$.
由$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$,得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$.
∴函数f(x)的单调区间是$[{kπ-\frac{π}{3},kπ+\frac{π}{6}}](k∈{Z})$.
(2)∵$x∈[{\frac{π}{12},\frac{π}{2}}]$,$f(x)=2sin({2x+\frac{π}{6}})$,
∴$2x+\frac{π}{6}∈[{\frac{π}{3},\frac{7π}{6}}]$.
当$2x+\frac{π}{6}=\frac{π}{2}$,即$x=\frac{π}{6}$时,f(x)取得最大值2;
当$2x+\frac{π}{6}=\frac{7π}{6}$,$x=\frac{π}{2}$时,f(x)取得最小值-1,故f(x)的值域为[-1,2].
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,属于基础题.

 名校课堂系列答案
名校课堂系列答案| A. | $-\frac{10}{3}$<λ≤$\frac{9}{4}$ | B. | $-\frac{10}{3}$<λ<$\frac{9}{4}$ | C. | $-\frac{9}{4}$<λ≤$\frac{10}{3}$ | D. | $-\frac{9}{4}$<λ<$\frac{10}{3}$ |
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
| A. | 0 | B. | 1 | C. | -1 | D. | 不存在 |
| A. | [1,+∞) | B. | [0,+∞) | C. | [3,+∞) | D. | R |
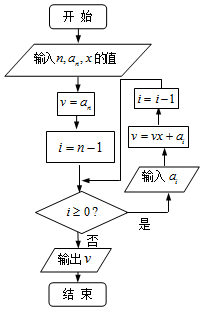 如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )
如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | -17 |