题目内容
16.已知sinα•cosα=$\frac{1}{8}$,且0<α<$\frac{π}{4}$,则sinα-cosα=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | -17 |
分析 由角的范围可求sinα-cosα<0,结合已知利用同角三角函数基本关系式即可计算得解.
解答 解:∵0<α<$\frac{π}{4}$,
∴sinα-cosα<0,
又∵sinα•cosα=$\frac{1}{8}$,
∴sinα-cosα=-$\sqrt{(sinα-cosα)^{2}}$=-$\sqrt{1-2sinαcosα}$=-$\sqrt{1-2×\frac{1}{8}}$=-$\frac{\sqrt{3}}{2}$.
故选:B.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
1.已知命题p:?x∈(-2,2),|x-1|+|x+2|≥6,则下列叙述正确的是( )
| A. | ¬p为:?x∈(-2,2),|x-1|+|x+2|<6 | B. | ¬p为:?x∈(-2,2),|x-1|+|x+2|≥6 | ||
| C. | ¬p为:?x∈(-∞,-2]∪[2,+∞),|x-1|+|x+2|<6 | D. | ¬p为真命题 |
5.设x,y满足约束条件$\left\{\begin{array}{l}2x+y-6≤0\\ x-y-1≤0\\ x-1≥0\end{array}\right.$,若z=ax+y仅在点$({\frac{7}{3},\frac{4}{3}})$处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
19.已知O为平面直角坐标系的原点,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,过双曲线左顶点A,做两渐近线的平行线分别与y轴交于C、D两点,B为双曲线的右顶点,若以O为圆心,|OF2|为直径的圆是四边形ACBD的内切圆,则装曲线的离心率为,( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
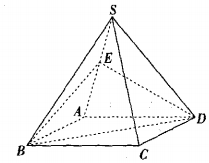 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明. 如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.
如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.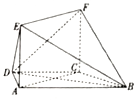 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.