题目内容
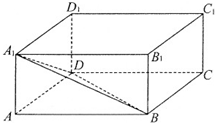 如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为
如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为考点:几何概型
专题:概率与统计
分析:根据几何概型的概率公式分别求出长方体和三棱锥A-A1BD的体积即可得到结论.
解答:
解:长方体的体积V=AA•AB•AD,
则三棱锥A-A1BD的体积为
×
AB•AD•AA1=
V,
∴由几何概型的概率公式可知动点在三棱锥A-A1BD内的概率为
=
,
故答案为:
.
则三棱锥A-A1BD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴由几何概型的概率公式可知动点在三棱锥A-A1BD内的概率为
| ||
| V |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题主要考查几何概型的概率计算,根据条件求出相应的体积是解决本题的关键.

练习册系列答案
相关题目
如图给出一个算法的程序框图,该程序框图的功能是( )
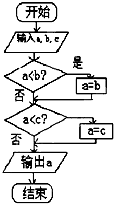

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
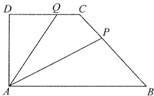 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,