题目内容
圆C:x2+y2-2x-4y-3=0的圆心坐标为 ;直线l:3x+4y+4=0与圆C位置关系是 .
考点:直线与圆的位置关系,圆的一般方程
专题:直线与圆
分析:将圆C方程化为标准方程,找出圆心C坐标即可;求出圆心C到直线l的距离d,与r比较大小即可得到位置关系.
解答:
解:圆C:x2+y2-2x-4y-3=0化为标准方程得:(x-1)2+(y-2)2=8,
∴圆心C(1,2),r=2
,
∵圆心C到直线3x+4y+4=0的距离d=
=3>2
=r,
∴直线l与圆C相离.
故答案为:(1,2);相离
∴圆心C(1,2),r=2
| 2 |
∵圆心C到直线3x+4y+4=0的距离d=
| |3+8+4| | ||
|
| 2 |
∴直线l与圆C相离.
故答案为:(1,2);相离
点评:此题考查了直线与圆的位置关系,以及圆的标准方程,直线与圆的位置关系由d与r的大小关系来判断,当d<r时,直线与圆相交;当d=r时,直线与圆相切;当d>r时,直线与圆相离(其中d表示圆心到直线的距离,r表示圆的半径).

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
认真阅读如图所示程序框图,则输出的S等于( )


| A、14 | B、20 | C、30 | D、55 |

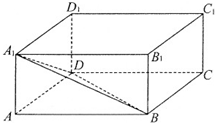 如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为
如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为