题目内容
12.已知函数f(x)=4x+$\frac{a}{x}$(x>0,a>0)在x=2时取得最小值,则实数a=16.分析 由基本不等式等号成立的条件和题意可得a的方程,解方程可得.
解答 解:∵x>0,a>0,∴f(x)=4x+$\frac{a}{x}$≥2$\sqrt{4x•\frac{a}{x}}$=4$\sqrt{a}$,
当且仅当4x=$\frac{a}{x}$即x=$\frac{\sqrt{a}}{2}$时取等号,
又∵f(x)在x=2时取得最小值,
∴$\frac{\sqrt{a}}{2}$=2,解得a=16,
故答案为:16.
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
4.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )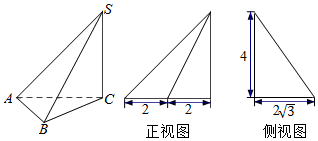

| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
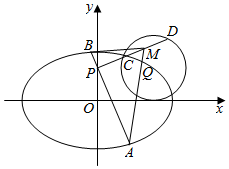 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.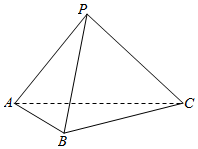 如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.
如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.