题目内容
14．已知函数g（x）=（$\frac{1}{2}$）|x-1|，则r=g（2-0.1），s=g（log0.23），t=g（2），则r，s，t的大小关系是（ ）| A． | t＜r＜s | B． | t＜s＜r | C． | s＜r＜t | D． | s＜t＜r |
分析 判断函数g（x）的对称性和单调性的关系进行转化比较即可．
解答 解：g（x）关于x=1对称，
当x＞1时，g（x）=（$\frac{1}{2}$）|x-1|=（$\frac{1}{2}$）x-1，为减函数，
当x≤1时，函数g（x）为增函数，
则0＜2-0.1＜1，log0.23＜0，t=g（2）=g（0），
则log0.23＜0＜2-0.1＜1，
∴g（log0.23）＜g（0）＜g（2-0.1），
即g（log0.23）＜g（2）＜g（2-0.1），
则s＜t＜r，
故选：D．
点评 本题主要考查函数值的大小比较，根据条件判断函数的单调性和对称性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（ ）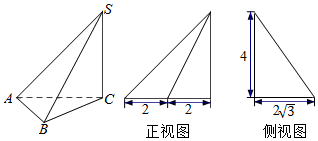
| A． | $16\sqrt{3}$ | B． | $\sqrt{38}$ | C． | $4\sqrt{2}$ | D． | $2\sqrt{11}$ |
9．设x，y为正实数，且x+y=1，则$\frac{{x}^{2}}{x+2}$+$\frac{{y}^{2}}{y+1}$的最小值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{4}{15}$ | D． | $\frac{1}{8}$ |