题目内容
9.在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2.(1)若椭圆C经过点($\frac{\sqrt{6}}{2}$,1),求椭圆C的标准方程;
(2)设A(-2,0),F为椭圆C的左焦点,若椭圆C上存在点P,满足$\frac{PA}{PF}$=$\sqrt{2}$,求椭圆C的离心率的取值范围.
分析 (1)由题意可得a2-b2=1,代入已知点,可得a,b的方程,解方程即可得到所求椭圆方程;
(2)设P(x,y),运用两点的距离公式,化简整理,即可得到P的轨迹方程,由题意和圆相交的条件,结合离心率公式,即可得到所求范围.
解答 解:(1)由题意可得c=1,即a2-b2=1,
又代入点($\frac{\sqrt{6}}{2}$,1),可得$\frac{3}{4{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
解方程可得a=$\sqrt{3}$,b=$\sqrt{2}$,
即有椭圆的方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1;
(2)由题意方程可得F(-1,0),
设P(x,y),由PA=$\sqrt{2}$PF,
可得$\sqrt{(x+2)^{2}+{y}^{2}}$=$\sqrt{2}$•$\sqrt{(x+1)^{2}+{y}^{2}}$,
化简可得x2+y2=2,
由c=1,即a2-b2=1,
由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和圆x2+y2=2有交点,
可得b2≤2≤a2,又b=$\sqrt{{a}^{2}-1}$,
可得$\sqrt{2}$≤a≤$\sqrt{3}$,
即有离心率e=$\frac{c}{a}$∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$].
点评 本题考查椭圆的方程的求法,注意运用方程的思想,考查轨迹方程的求法,以及椭圆和圆相交的关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.设函数f(x)是定义在R上的奇函数,当x∈(0,1]时f(x)=1+log2x.若对任意的x∈R都有f(x)=f(x+4),则f(2014)+f(2016)-2f(2015)=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
4.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )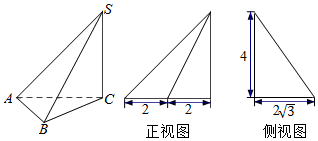

| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
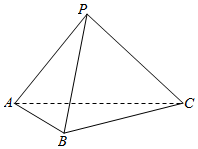 如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.
如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.