题目内容
13．若函数f（x）是奇函数．且在x＞0时是增函数，则下列结论中正确的是（ ）| A． | f（-1）＜f（-2）＜f（-3） | B． | f（-3）＜f（-2）＜f（-1） | C． | f（-2）＜f（-1）＜f（-3） | D． | f（-3）＜f（-1）＜f（-2） |
分析 根据函数奇偶性的性质以及函数奇偶性和单调性的关系进行判断即可．
解答 解：∵函数f（x）是奇函数，且在x＞0时是增函数，
∴当x＜0时函数f（x）是增函数，
则f（-3）＜f（-2）＜f（-1），
故选：B．
点评 本题主要考查函数值的大小比较，根据函数奇偶性和单调性的关系进行转化是解决本题的关键．
练习册系列答案
相关题目
4．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（ ）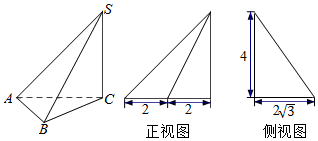
| A． | $16\sqrt{3}$ | B． | $\sqrt{38}$ | C． | $4\sqrt{2}$ | D． | $2\sqrt{11}$ |
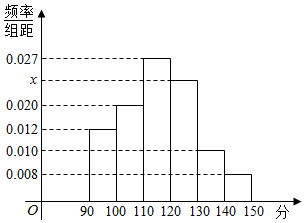某校高一年级为组建数学兴趣小组，对参加报名的100名同进行了摸底考试，发现其成绩都在90-150分之间．频率分布直方图如图所示