题目内容
16．若a=$\frac{1-cosα}{sinα}$，b=$\frac{1+cosα}{sinα}$，则ab的值是（ ）| A． | 0 | B． | 1 | C． | -1 | D． | $\sqrt{2}$ |
分析 根据题意，将a、b的值代入ab中可得，ab=$\frac{1-co{s}^{2}α}{si{n}^{2}α}$=$\frac{si{n}^{2}α}{si{n}^{2}α}$，化简可得答案．
解答 解：根据题意，a=$\frac{1-cosα}{sinα}$，b=$\frac{1+cosα}{sinα}$，
则ab=$\frac{1-cosα}{sinα}$×$\frac{1+cosα}{sinα}$=$\frac{（1-cosα）（1+cosα）}{si{n}^{2}α}$=$\frac{1-co{s}^{2}α}{si{n}^{2}α}$=$\frac{si{n}^{2}α}{si{n}^{2}α}$=1；
故选：B．
点评 本题考查同角三角函数基本关系式的运用，关键是掌握同角三角函数基本关系式并灵活运用．
练习册系列答案
相关题目
6．对于直线m，n和平面α，β，能得出α⊥β的一个条件是（ ）
| A． | m⊥n，m∥α，n∥β | B． | m⊥n，α∩β=m，n?α | C． | m∥n，n⊥β，m?α | D． | m∥n，m⊥α，n⊥β |
4．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（ ）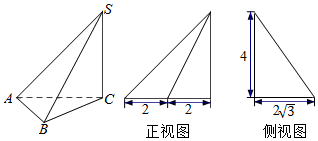
| A． | $16\sqrt{3}$ | B． | $\sqrt{38}$ | C． | $4\sqrt{2}$ | D． | $2\sqrt{11}$ |
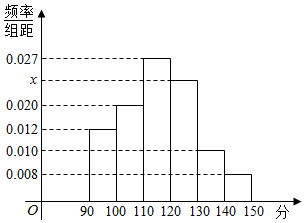某校高一年级为组建数学兴趣小组，对参加报名的100名同进行了摸底考试，发现其成绩都在90-150分之间．频率分布直方图如图所示