题目内容
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=
(an+
).
(1)求出a1,a2,a3的值.
(2)由(1)猜想数列{an}的通项公式,并证明你的结论.
| 1 |
| 2 |
| 1 |
| an |
(1)求出a1,a2,a3的值.
(2)由(1)猜想数列{an}的通项公式,并证明你的结论.
考点:数学归纳法,数列递推式
专题:计算题,点列、递归数列与数学归纳法
分析:(1)由Sn=
(an+
),代入n=1,2,计算,可求a1,a2,a3的值;
(2)猜想{an}的通项公式,再用数学归纳法证明,关键是假设当n=k(k≥1)时,命题成立,即成立,利用递推式,证明当n=k+1时,等式成立.
| 1 |
| 2 |
| 1 |
| an |
(2)猜想{an}的通项公式,再用数学归纳法证明,关键是假设当n=k(k≥1)时,命题成立,即成立,利用递推式,证明当n=k+1时,等式成立.
解答:
解:(1)S1=a1=
(a1+
),得
=1,由an>0,∴a1=1.(1分)
S2=a1+a2=
(a2+
),得
+2a2-1=0,∴a2=
-1,(3分)
同理,求得a3=
-
.(5分)
(2)猜想an=
-
(n∈N*).(6分)
①n=1时,a1=
-
命题成立.(7分)
②假设n=k时,ak=
-
(k∈N*)(*)成立,
则n=k+1时,ak+1=Sk+1-Sk=
(ak+1+
)-
(ak+
)
把 (*)代入上式,化简得,ak+12+2
ak+1-1=0,
∴ak+1=
-
(负舍),即n=k+1时,命题成立.
由①②得,an=
-
(n∈N*).(14分)
| 1 |
| 2 |
| 1 |
| a1 |
| a | 2 1 |
S2=a1+a2=
| 1 |
| 2 |
| 1 |
| a2 |
| a | 2 2 |
| 2 |
同理,求得a3=
| 3 |
| 2 |
(2)猜想an=
| n |
| n-1 |
①n=1时,a1=
| 1 |
| 0 |
②假设n=k时,ak=
| k |
| k-1 |
则n=k+1时,ak+1=Sk+1-Sk=
| 1 |
| 2 |
| 1 |
| ak+1 |
| 1 |
| 2 |
| 1 |
| ak |
把 (*)代入上式,化简得,ak+12+2
| k |
∴ak+1=
| k+1 |
| k |
由①②得,an=
| n |
| n-1 |
点评:本题考查数列的通项,考查归纳猜想,考查数学归纳法的运用,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
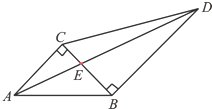 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.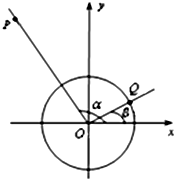 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为