题目内容
2.求证:k•${C}_{n}^{k}$=n•${C}_{n-1}^{k-1}$(n,k∈N*,k≤n)分析 直接利用组合数公式化简证明即可.
解答 证明:k•${C}_{n}^{k}$=$\frac{k•n!}{(n-k)!•k!}$=$\frac{n•(n-1)!}{(n-1-k+1)!•(k-1)!}$=n•${C}_{n-1}^{k-1}$,
等式成立.
点评 本题考查组合式公式的应用,考查计算能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
13.等比数列{an}满足a1=1,且$\frac{1}{{a}_{1}}$,$\frac{1}{{a}_{2}}$,$\frac{1}{{a}_{3}}$成等差数列,则数列{an}的前10项和为( )
| A. | 10 | B. | 20 | C. | 256 | D. | 510 |
17.已知数列{an}满足a1=4,an+1=2an+2n+1,那么数列{an}的通项公式是( )
| A. | an=2n | B. | an=(n+1)•2n | C. | an=(n-1)•2n | D. | an=3n-1 |
7.在?ABCD中,已知$\overrightarrow{AC}$=(-4,2),$\overrightarrow{BD}$=(2,-6),那么|2$\overrightarrow{AB}$+$\overrightarrow{AD}$|=( )
| A. | 5$\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{85}$ |
14.若α∈(0,$\frac{π}{3}$),则${5}^{{|log}_{5}(cosα)|}$=( )
| A. | cosα | B. | $\frac{1}{cosα}$ | C. | -cosα | D. | -$\frac{1}{cosα}$ |
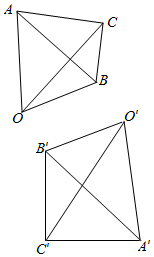 如图所示,有点O,O′和△A′B′C′,满足下列条件:$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{O{{\;}^{'}A}^{'}}$=-$\overrightarrow{a}$,$\overrightarrow{O{{\;}^{'}B}^{'}}$=-$\overrightarrow{b}$,O′C′=-$\overrightarrow{c}$,求证:△ABC≌△A′B′C′.
如图所示,有点O,O′和△A′B′C′,满足下列条件:$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{O{{\;}^{'}A}^{'}}$=-$\overrightarrow{a}$,$\overrightarrow{O{{\;}^{'}B}^{'}}$=-$\overrightarrow{b}$,O′C′=-$\overrightarrow{c}$,求证:△ABC≌△A′B′C′.