题目内容
16.函数$f(x)=x-\sqrt{2}sinx$在区间[0,π]上的最大、最小值分别为( )| A. | π,0 | B. | $\frac{π}{2}-\sqrt{2}\;,0$ | C. | $π\;,\frac{π}{4}-1$ | D. | $0\;,\;\frac{π}{4}-1$ |
分析 对函数f(x)求导数,利用导数判断f(x)的单调性,并求f(x)在区间[0,π]上的最大、最小值.
解答 解:函数$f(x)=x-\sqrt{2}sinx$,
∴f′(x)=1-$\sqrt{2}$cosx;
令f′(x)=0,解得cosx=$\frac{\sqrt{2}}{2}$,
又x∈[0,π],∴x=$\frac{π}{4}$;
∴x∈[0,$\frac{π}{4}$)时,f′(x)<0,f(x)单调递减;
x∈($\frac{π}{4}$,π]时,f′(x)>0,f(x)单调递增;
且f($\frac{π}{4}$)=$\frac{π}{4}$-$\sqrt{2}$sin$\frac{π}{4}$=$\frac{π}{4}$-1,
f(0)=0,f(π)=π;
∴函数f(x)在区间[0,π]上的最大、最小值分别为π和$\frac{π}{4}$-1.
故选:C.
点评 本题考查了利用导数求函数在闭区间上的最值问题,是中档题.

练习册系列答案
相关题目
7.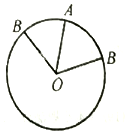 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
11.等差数列{an}的前n项和为Sn,已知a19+2a20+a21=4,则S39=( )
| A. | 38 | B. | 39 | C. | 20 | D. | 19 |
8.曲线y=-x3+3x2在点(1,2)处的切线方程为( )
| A. | y=-3x+5 | B. | y=3x-1 | C. | y=3x+5 | D. | y=2x |
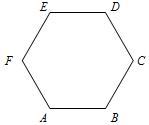 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.