题目内容
已知数列{an}的前n项和为Sn,a1=1,且2nSn+1-2(n+1)Sn=n(n+1)(n∈N*).数列{bn}满足bn+2-2bn+1+bn=0(n∈N*).b3=5,其前9项和为63.
(1)求数列{an}和{bn}的通项公式;
(2)令cn=
+
,数列{cn}的前n项和为Tn,若对任意正整数n,都有Tn-2n∈[a,b],求b-a的最小值.
(1)求数列{an}和{bn}的通项公式;
(2)令cn=
| bn |
| an |
| an |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由2nSn+1-2(n+1)Sn=n(n+1)(n∈N*),变形
-
=
,可得数列{
}是等差数列,利用等差数列的通项公式可得
,Sn=
.再利用“当n≥2时,an=Sn-Sn-1,当n=1时也成立”即可得出an.由于数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),可得数列{bn}是等差数列,利用等差数列的通项公式及其前n选和公式即可得出.
(2)cn=
+
=
+
=2+2(
-
),利用“裂项求和”可得:数列{cn}的前n项和为Tn=3+2n-2(
+
).设An=3-2(
+
),可得数列{An}单调递增,得出:
≤An<3.由于对任意正整数n,都有Tn-2n∈[a,b],可得a≤
,b≥3,即可得出.
| Sn+1 |
| n+1 |
| Sn |
| n |
| 1 |
| 2 |
| Sn |
| n |
| Sn |
| n |
| n(n+1) |
| 2 |
(2)cn=
| bn |
| an |
| an |
| bn |
| n+2 |
| n |
| n |
| n+2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 4 |
| 3 |
| 4 |
| 3 |
解答:
解:(1)∵2nSn+1-2(n+1)Sn=n(n+1)(n∈N*),∴
-
=
,∴数列{
}是等差数列,首项为1,公差为
,∴
=1+
(n-1),
∴Sn=
.∴当n≥2时,Sn-1=
,an=Sn-Sn-1=
-
=n,当n=1时也成立.∴an=n.
∵数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),∴数列{bn}是等差数列,设公差为d,∵前9项和为63,∴
=9b5=63,解得b5=7,又b3=5,
∴d=
=1,∴bn=b3+(n-3)d=5+n-3=n+2,∴bn=n+2.
因此:an=n,bn=n+2.
(2)cn=
+
=
+
=2+2(
-
),
∴数列{cn}的前n项和为Tn=2n+2[(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=2n+2(1+
-
-
)
=3+2n-2(
+
).
∴Tn-2n=3-2(
+
).
设An=3-2(
+
),
∵An+1-An=3-2(
+
)-3+2(
+
)=2(
-
)>0,
∴数列{An}单调递增,
∴(An)min=A1=
.
而An<3,
∴
≤An<3.
∵对任意正整数n,都有Tn-2n∈[a,b],
∴∴a≤
,b≥3,
∴b-a的最小值=3-
=
.
| Sn+1 |
| n+1 |
| Sn |
| n |
| 1 |
| 2 |
| Sn |
| n |
| 1 |
| 2 |
| Sn |
| n |
| 1 |
| 2 |
∴Sn=
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
∵数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),∴数列{bn}是等差数列,设公差为d,∵前9项和为63,∴
| 9(b1+b9) |
| 2 |
∴d=
| b5-b3 |
| 2 |
因此:an=n,bn=n+2.
(2)cn=
| bn |
| an |
| an |
| bn |
| n+2 |
| n |
| n |
| n+2 |
| 1 |
| n |
| 1 |
| n+2 |
∴数列{cn}的前n项和为Tn=2n+2[(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=2n+2(1+
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=3+2n-2(
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Tn-2n=3-2(
| 1 |
| n+1 |
| 1 |
| n+2 |
设An=3-2(
| 1 |
| n+1 |
| 1 |
| n+2 |
∵An+1-An=3-2(
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+3 |
∴数列{An}单调递增,
∴(An)min=A1=
| 4 |
| 3 |
而An<3,
∴
| 4 |
| 3 |
∵对任意正整数n,都有Tn-2n∈[a,b],
∴∴a≤
| 4 |
| 3 |
∴b-a的最小值=3-
| 4 |
| 3 |
| 5 |
| 3 |
点评:本题考查了递推式的应用、等差数列的通项公式及前n项和公式及其性质、“裂项求和”、数列的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合M={0,1,2},N={x},若M∪N={0,1,2,3},则x的值为( )
| A、3 | B、2 | C、1 | D、0 |
下列命题中的假命题是( )
| A、?x∈R,lnx=0 |
| B、?x∈R,sinx+cosx=1 |
| C、?x∈R,x3>0 |
| D、?x∈R,3x>0 |
已知实数x,y满足
,则z=x-y的最小值为( )
|
| A、1 | B、-1 | C、2 | D、-2 |
 已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E. 某校学生在一次学业水平测试中的数学成绩制成如图所示频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为
某校学生在一次学业水平测试中的数学成绩制成如图所示频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为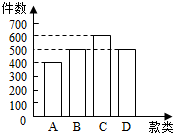 随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表:
随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表: