题目内容
已知数列{an}的前n项和为Sn=2n-1,n∈N*
(1)求数列{an}的通项公式;
(2)设数列bn=
,试求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设数列bn=
| 1 |
| log2an+1•log2an+2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由于数列{an}的前n项和为Sn=2n-1,n∈N*.利用“当n≥2时,an=Sn-Sn-1,当n=1时,a1=S1”即可得出.
2)bn=
=
-
,利用“裂项求和”即可得出.
2)bn=
| 1 |
| n•(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)∵数列{an}的前n项和为Sn=2n-1,n∈N*.
∴当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1.
当n=1时,a1=S1=2-1=1,上式也满足.
∴an=2n-1.
(2)bn=
=
=
-
,
则数列{bn}的前n项和Tn=(1-
)+(
-
)+…+(
-
)=1-
=
.
∴当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1.
当n=1时,a1=S1=2-1=1,上式也满足.
∴an=2n-1.
(2)bn=
| 1 |
| log2an+1•log2an+2 |
| 1 |
| n•(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则数列{bn}的前n项和Tn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了递推式的应用、对数的运算性质、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知集合M={x|x2-2x-3<0},N={x|y=
},则M∩N=( )
| 1 | ||
|
| A、[1,3) |
| B、(1,3] |
| C、(-1,+∞) |
| D、(1,3) |
已知双曲线
-2y2=1(a>0)的右焦点与抛物线y2=4x的焦点重合,则此双曲线的渐近线方程是( )
| x2 |
| a2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±x |
若方程
+
=1表示双曲线,则实数k的取值范围是( )
| x2 |
| 1+k |
| y2 |
| 1-k |
| A、k<-1 |
| B、k>1 |
| C、-1<k<1 |
| D、k<-1或k>1 |
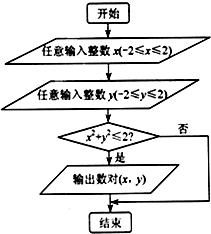 执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )
执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:?x∈(0,+∞),log2x<log3x.命题q:?x∈R,x3=1-x2.则下列命题中为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、p∧¬q | D、¬p∧¬q |