题目内容
已知函数f(x)=x-2x2+alnx(a是常数).
(Ⅰ)当a=1时,求f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证若函数f(x)在区间[
,3]上为单调函数,求a的取值范围.
(Ⅰ)当a=1时,求f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证若函数f(x)在区间[
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:常规题型
分析:(Ⅰ)利用原函数求纵坐标,利用导函数求切线的斜率,利用点斜式求出切线方程;
(Ⅱ)已知原函数在区间上单调,得到导函数在区间上的值恒为正或者恒为负,得到相应函数的最大值小于零,或者最小值大于零,从而求出参数的取值范围,即得到本题的解.
(Ⅱ)已知原函数在区间上单调,得到导函数在区间上的值恒为正或者恒为负,得到相应函数的最大值小于零,或者最小值大于零,从而求出参数的取值范围,即得到本题的解.
解答:
解:(Ⅰ)当a=1时,f(x)=x-2x2+lnx,f'(x)=1-4x+
,
当x=1时,f(1)=-1,f'(1)=-2.
∴当x=1时,f(x)在点(1,f(1))处的切线方程为:y+1=-2(x-1).
即切线方程为:2x+y-1=0.
(Ⅱ)∵f(x)=x-2x2+alnx,
∴f'(x)=1-4x+
=
(x>0).
∵函数f(x)在区间[
,3]上为单调函数,
∴f'(x)在区间[
,3]上的值恒为正,或者值恒为负.
记g(x)=-4x2+x-a,
则g(x)在区间[
,3]上的值恒为正,或者值恒为负.
∵g(x)=-4x2+x-a的图象开口向下,对称轴为:x=
,
∴g(
)≤0或者g(3)≥0,
故有:a≤
或 a≥33.
| 1 |
| x |
当x=1时,f(1)=-1,f'(1)=-2.
∴当x=1时,f(x)在点(1,f(1))处的切线方程为:y+1=-2(x-1).
即切线方程为:2x+y-1=0.
(Ⅱ)∵f(x)=x-2x2+alnx,
∴f'(x)=1-4x+
| a |
| x |
| -4x2+x-a |
| x |
∵函数f(x)在区间[
| 1 |
| 2 |
∴f'(x)在区间[
| 1 |
| 2 |
记g(x)=-4x2+x-a,
则g(x)在区间[
| 1 |
| 2 |
∵g(x)=-4x2+x-a的图象开口向下,对称轴为:x=
| 1 |
| 8 |
∴g(
| 1 |
| 2 |
故有:a≤
| 1 |
| 2 |
点评:本题考查的是导数知识,包括利用导数求切线方程,利用导数研究原函数的单调区间,还涉及到恒成立的问题,考查了学生分析问题解决问题的能力.本题有一定的思维量和计算量,属于中档题.

练习册系列答案
相关题目
认真阅读如图所示程序框图,则输出的S等于( )


| A、14 | B、20 | C、30 | D、55 |
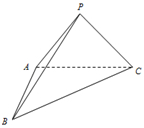 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=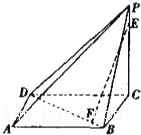 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.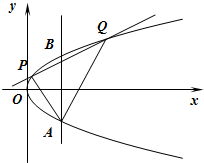 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=