题目内容
5．设集合U={x|x2-3x+2=0，x∈R}，则集合U的子集的个数是4．分析 解方程求出U的元素，从而求出其子集的个数即可．
解答 解：U={x|x2-3x+2=0，x∈R}={1，2}，
则集合U的子集的个数是：22=4，
故答案为：4．
点评 本题考查了求集合的子集问题，是一道基础题．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
13．已知实数x，y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}$，则2y•（$\frac{1}{4}$）x的最小值是（ ）
| A． | 1 | B． | 2 | C． | 8 | D． | 4 |
20．下列四组函数中，表示同一个函数的是（ ）
| A． | f（x）=|x+1|，g（x）=$\left\{\begin{array}{l}{x+1（x≥-1）}\\{-1-x（x＜-1）}\end{array}\right.$ | B． | f（x）=$\frac{{x}^{2}-1}{x+1}$，g（x）=x-1 | ||
| C． | f（x）=$\sqrt{{x}^{2}}$，g（x）=（$\sqrt{x}$）2 | D． | f（x）=x，g（x）=$\sqrt{{x}^{2}}$ |
10．
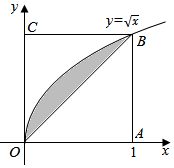如图所示，在边长为1的正方形OABC内任取一点P，用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”，B表示事件“点P恰好取自阴影部分内”，则P（B|A）等于（ ）
如图所示，在边长为1的正方形OABC内任取一点P，用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”，B表示事件“点P恰好取自阴影部分内”，则P（B|A）等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{7}$ |
17．若点（1，-3）在圆（x-2）2+（y+1）2=m的内部，则实数m的取值范围是（ ）
| A． | 0＜m＜10 | B． | 0＜m＜5 | C． | m＞5 | D． | m＜5 |
14．若函数f（x）=xlnx-ax2有两个极值点，则实数a的取值范围是（ ）
| A． | $（{0，\frac{1}{2}}）$ | B． | $（{\frac{1}{2}，1}）$ | C． | （1，2） | D． | （2，e） |