题目内容
15.已知直线l:y=x+m,圆O:x2+y2-4=0,圆C:x2+y2+2ax-2ay+2a2-4a=0(0<a≤4).(1)若a=3,圆O与圆C交于M,N两点,试求线段|MN|的长.
(2)直线 l与圆C相切,且直线l在圆C心的下方,当0<a≤4时,求m的取值范围.
分析 (1)由方程x2+y2-4=0与x2+y2+6x-6y+6=0消去二次项得,3x-3y+5=0,再求得圆心O到直线3x-3y+5=0的距离,由圆弦长、圆心距和圆的半径之间关系得线段|MN|的长;
(2)由直线l与圆C相切,建立m与a的关系$\frac{{|{m-2a}|}}{{\sqrt{2}}}=2\sqrt{a}$,再由点C在直线l的上方,去掉绝对值,将m转化为关于a二次函数求解.
解答 解:(1)当a=3时,C:x2+y2+6x-6y+6=0,由方程x2+y2-4=0与x2+y2+6x-6y+6=0消去二次项得,3x-3y+5=0,圆心O到直线3x-3y+5=0的距离为$d=\frac{{|{0-0+5}|}}{{\sqrt{9+9}}}=\frac{{5\sqrt{2}}}{6}$,∴$|{MN}|=2\sqrt{4-\frac{25}{18}}=\frac{{\sqrt{94}}}{3}$.
(2)∵x2+y2+2ax-2ay+2a2-4a=0,∴(x+a)2+(y-a)2=4a,∴圆心C(-a,a),半径$r=2\sqrt{a}$,
圆心C(-a,a)到直线l的距离为$d=\frac{{|{-a-a+m}|}}{{\sqrt{2}}}=\frac{{|{m-2a}|}}{{\sqrt{2}}}$,
∵直线l与圆C2相切,∴d=r,即$\frac{{|{m-2a}|}}{{\sqrt{2}}}=2\sqrt{a}$,∴$m=2a±2\sqrt{2a}$,
∵直线l在圆心C的下方,∴$m=2a-2\sqrt{2a}={({\sqrt{2a}-1})^2}-1$,∵0<a≤4,
∴$m∈[{-1,8-4\sqrt{2}}]$.
点评 本题主要考查直线与圆的位置关系及其方程的应用,主要涉及了直线与圆相交,由圆心距,半径和圆的弦长构成的直角三角形.

 综合自测系列答案
综合自测系列答案| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
| x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
| y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程:$\widehat{y}$=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据$\sum_{i=1}^{5}$(yi-$\widehat{y}$i)2=1.15)
参考公式:相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘法估计公式分别为$\widehat{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,参考数据:ln40=3.688,${\sum_{i=1}^5{({x_i}-\overline x)}^2}$=538.
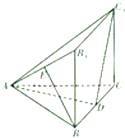 如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.
如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.