Question

20．已知函数f（x）=x|x-1|
（1）画出该函数的图象；
（2）求函数f（x）的单调区间；
（3）设0＜a＜1，求f（x）在[0，a]上的最大值．

Answer 1

分析 （1）化简函数，利用二次函数图象的作法，可得该函数的图象；
（2）根据图象求函数f（x）的单调区间；
（3）设0＜a＜1，分类讨论，即可求f（x）在[0，a]上的最大值．

解答 解：（1）f（x）=$\left\{\begin{array}{l}{{x}^{2}-x（x≥1）}\\{x-{x}^{2}（x＜1）}\end{array}\right.$，如图所示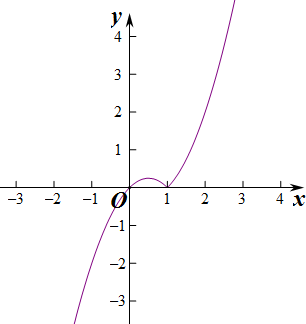

$（2）由图象得函数f（x）的单调增区间为（{-∞，\frac{1}{2}}），（{1，+∞}）；减区间为（{\frac{1}{2}，1}）$；
$（3）当0＜a＜\frac{1}{2}时，f（x）在[{0，a}]上，f{（x）_{max}}=f（a）=a-{a^2}$；
$当\frac{1}{2}≤a＜1时，f（x）在[{0，a}]上，f{（x）_{max}}=f（\frac{1}{2}）=\frac{1}{4}$．

点评 本题考查函数的图象，并根据图象研究函数的性质，考查学生分析解决问题的能力，属于中档题．