题目内容
11．已知x，y满足约束条件$\left\{\begin{array}{l}x≥1\\ x-3y≤-4\\ 3x+5y≤30.\end{array}\right.$．（1）画出函数的可行域，求目标函数z=2x+y的最大值；
（2）求z=$\frac{y+5}{x+5}$的最大值．
分析 （1）作出函数的可行域，如图所示，确定出A，B，C的坐标，当l过点C时，z最大值，求出最大值即可；
（2）z表示点D与（x，y）连线的斜率，当点（x，y）为点C时，直线CD斜率最大，求出最大值即可．
解答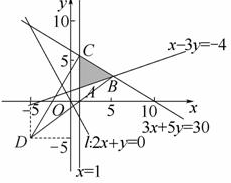 
解：（1）可行域如图所示：由题意得：A（1，$\frac{5}{3}$），B（5，3），C（1，$\frac{27}{5}$），
当z=2x+y过点B时，取得最大值，最大值为z=2x+y=2×5+3=13；
（2）z=$\frac{y+5}{x+5}$表示点D（-5，-5）与点（x，y）的连线斜率，
当点（x，y）为点C（1，$\frac{27}{5}$）时，直线CD斜率最大，最大值为$\frac{\frac{27}{5}-（-5）}{1-（-5）}$=$\frac{26}{15}$．
点评 此题考查了简单线性规划，正确作出函数的可行域是解本题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
7．已知等比数列{an}的各项均为正数，且满足a3=a1+2a2，则$\frac{{a}_{9}+{a}_{10}}{{a}_{7}+{a}_{8}}$等于（ ）
| A． | 2+3$\sqrt{2}$ | B． | 2+2$\sqrt{2}$ | C． | 3-2$\sqrt{2}$ | D． | 3+2$\sqrt{2}$ |
3．已知a＞0，且a≠1，下列函数中，在其定义域内是单调函数而且又是奇函数的是（ ）
| A． | y=sinax | B． | y=logax2 | C． | y=ax-a-x | D． | y=tanax |
已知函数f（x）=x|x-1|