题目内容
9.已知奇函数f(x)在区间[-1,1]上是增函数,且f(1)=1,若函数f(x)≥t2-4at-1对所有的x∈[-1,1]都存在a∈[-1,1]使不等式成立,则实数t的取值范围是{0}}.分析 由f(1)=1得f(-1)=-1,f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,只需要f(x)的最小值大于或等于t2-4at+1即可.再利用二次函数的性质求得t的范围.
解答 解:∵函数f(x)是奇函数,且在[-1,1]是单调增函数,又f(1)=1,∴f(-1)=-1,
∴当x∈[-1,1]时,f(x)∈[-1,1].
若函数f(x)≥t2-4at-1对所有的x∈[-1,1]都成立,由已知易得f(x)的最小值是-1,
∴-1≥t2-4at-1,等价于t2-4at≤0.
设g(a)=t2-4at(-1≤a≤1),
欲使 t2-4at≤0恒成立,则 $\left\{\begin{array}{l}{g(-1){=t}^{2}+4t≤0}\\{g(1){=t}^{2}-4t≤0}\end{array}\right.$,求得t=0,
故答案为:{0}.
点评 本题考查的知识点是奇偶性与单调性的综合,其中根据已知结合函数的奇偶性与单调性判断出当x∈[-1,1]时,函数f(x)值域,是解答本题的关键,考查了函数的恒成立问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.2016°角所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.函数f(x)=$\frac{x}{(1-x)^{2}}$的单调递增区间是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
 已知函数f(x)=x|x-1|
已知函数f(x)=x|x-1|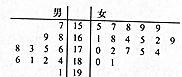 某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):