题目内容
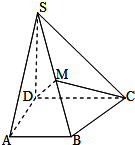 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设PA=k•AB,且二面角E-BD-C为60°,求k的值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件得ABFD是矩形,BF=CD,由三垂线定理,得PD⊥CD,由此能证明CD⊥平面BEF.
(Ⅱ)连结AC,交BF于H,则H是AC中点,连结EH,作HM⊥BD于M,连结EM,由已知条件得∠EMH为二面角E-BD-F的平面角,由此能求出k.
(Ⅱ)连结AC,交BF于H,则H是AC中点,连结EH,作HM⊥BD于M,连结EM,由已知条件得∠EMH为二面角E-BD-F的平面角,由此能求出k.
解答:
(Ⅰ)证明:∵DF∥AB,DF=AB,∠DAB=90°,
∴ABFD是矩形,∴BF=CD,
∵PA⊥平面ABCD,AD⊥CD,
∴由三垂线定理,得PD⊥CD,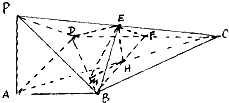
∵E是PC中点,F是CD中点,∴EF∥PD,
∴EF⊥CD,∴CD⊥平面BEF.
(Ⅱ)解:连结AC,交BF于H,则H是AC中点,连结EH,
由E是PC中点,得EH∥PA,PA⊥平面ABCD,
得EH⊥平面ABCD,且EH=
PA=
,
作HM⊥BD于M,连结EM,由三垂直线定理得EM⊥BD,
∴∠EMH为二面角E-BD-F的平面角,∴∠EMH=60°,
∵Rt△HBM∽Rt△DBF,
∴
=
,∴
=
,解得HM=
,
在Rt△EHM中,
=tan60°,
∴
=
,解得k=
.
∴ABFD是矩形,∴BF=CD,
∵PA⊥平面ABCD,AD⊥CD,
∴由三垂线定理,得PD⊥CD,

∵E是PC中点,F是CD中点,∴EF∥PD,
∴EF⊥CD,∴CD⊥平面BEF.
(Ⅱ)解:连结AC,交BF于H,则H是AC中点,连结EH,
由E是PC中点,得EH∥PA,PA⊥平面ABCD,
得EH⊥平面ABCD,且EH=
| 1 |
| 2 |
| k |
| 2 |
作HM⊥BD于M,连结EM,由三垂直线定理得EM⊥BD,
∴∠EMH为二面角E-BD-F的平面角,∴∠EMH=60°,
∵Rt△HBM∽Rt△DBF,
∴
| HM |
| DF |
| HB |
| BD |
| HM |
| 1 |
| 1 | ||
|
| 1 | ||
|
在Rt△EHM中,
| EH |
| HM |
∴
| ||
| 2 |
| 3 |
2
| ||
| 5 |
点评:本小题主要考查直线与直线、直线与平面、平面与平面等基础知识,考查空间想象能力、推理论证能力、运算求解能力等,考查化归与转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在数列{an}中,已知a3=1,a5=3,a7=9,则{an}一定( )
| A、是等差数列 |
| B、是等比数列 |
| C、不是等差数列 |
| D、不是等比数列 |