题目内容
已知函数f（x）=2ax+xlnx的图象在x=e处的斜率为4，证明：当x＞1时，f（x）-4x+3＞0恒成立．
考点：利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：利用导数的几何意义，求出切线斜率求出a的值，然后利用导数构造函数，求出函数的最值即可得到结论．
解答：
解：（1）∵f（x）=2ax+xlnx，
∴f′（x）=2a+lnx+1，
∵函数f（x）=ax+xlnx的图象在点x=e处的切线斜率为4，
∴f′（e）=4，∴2a+lne+1=4，
即2a=2．∴a=1．
∴f（x）=2x+xlnx，
令g（x）=f（x）-4x+3=xlnx-2x+3，
则g′（x）=lnx+1-2=lnx-1，
由g′（x）＞0，解得x＞e，此时函数递增，
由g′（x）＜0，解得1＜x＜e，此时函数递减，
故x=e时函数g（x）取得极小值，同时也是最小值g（e）=elne-2e+3=3-e＞0恒成立．
∴f′（x）=2a+lnx+1，
∵函数f（x）=ax+xlnx的图象在点x=e处的切线斜率为4，
∴f′（e）=4，∴2a+lne+1=4，
即2a=2．∴a=1．
∴f（x）=2x+xlnx，
令g（x）=f（x）-4x+3=xlnx-2x+3，
则g′（x）=lnx+1-2=lnx-1，
由g′（x）＞0，解得x＞e，此时函数递增，
由g′（x）＜0，解得1＜x＜e，此时函数递减，
故x=e时函数g（x）取得极小值，同时也是最小值g（e）=elne-2e+3=3-e＞0恒成立．
点评：本题主要考查导数的几何意义，利用导数研究函数的极值和最值，构造函数时解决本题的关键．
练习册系列答案
相关题目
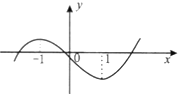已知函数f（x）=ax3+bx2+cx+d图象如图所示，f′（x）是f（x）的导函数，则不等式| f′(x) |
| x |
| A、（-∞，-1）∪（0，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-1，0）∪（0，1） |
| D、（-1，0）∪（1，+∞） |
如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AA1=2，AC=2，E为A1C!中点，求直线CC1与平面BCE所成角的大小．（结果用反三角函数值表示）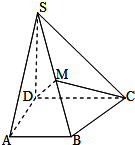
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠DAB=90°，AB∥CD，AD=CD=2AB=2，E，F分别是PC，CD的中点．