题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,向量
=(cosBcosC,sinBsinC-
),
=(-1,1)且
⊥
.
(Ⅰ)求A的大小;
(Ⅱ)若a=1,B=45°,求△ABC的面积.
| m |
| ||
| 2 |
| n |
| m |
| n |
(Ⅰ)求A的大小;
(Ⅱ)若a=1,B=45°,求△ABC的面积.
考点:正弦定理,平面向量的综合题
专题:解三角形
分析:(Ⅰ)先根据向量垂直建立等式求得cosA的值,进而求得A.
(Ⅱ)先利用两角和公式求得sinC的值,进而利用正弦定理求得c,最后利用三角形面积公式求得答案.
(Ⅱ)先利用两角和公式求得sinC的值,进而利用正弦定理求得c,最后利用三角形面积公式求得答案.
解答:
解:(Ⅰ)∵
⊥
,
∴-cosBcosC+sinBsinC-
=0,即cosBcosC-sinBsinC=cos(B+C)=-cosA=-
,
∴A=30°.
(Ⅱ)sinC=sin(18°-A-B)=sin(30°+45°)=sin30°cos45°+cos30°sin45°=
×
+
×
=
,
由正弦定理知c=
=
=
,
∴S=
acsinB=
×1×
=
.
| m |
| n |
∴-cosBcosC+sinBsinC-
| ||
| 2 |
| ||
| 2 |
∴A=30°.
(Ⅱ)sinC=sin(18°-A-B)=sin(30°+45°)=sin30°cos45°+cos30°sin45°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |
由正弦定理知c=
| asinC |
| sinA |
| sin105°•1 |
| sin30° |
| ||||
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 4 |
点评:本题主要考查了正弦定理的应用,三角函数恒等变换的应用,平面向量的基础知识.综合考查了学生运用基础知识的能力.

练习册系列答案
相关题目
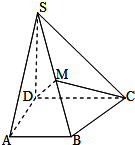 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.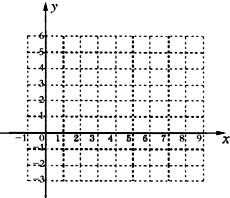 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<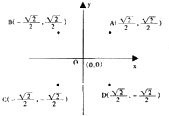 如图,A(
如图,A(