题目内容
已知f(x)=xn+xn-1+…+x-1(x∈(0,+∞),n∈N,n≥2).
(1)当n=2,x∈(0,1]时,若不等式f(x)≤kx恒成立,求k的范围;
(2)试证函数f(x)在(
,1)内存在零点.
(1)当n=2,x∈(0,1]时,若不等式f(x)≤kx恒成立,求k的范围;
(2)试证函数f(x)在(
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:函数的性质及应用,导数的概念及应用,等差数列与等比数列
分析:(1)将n=2带入原函数求出f(x),带入不等式便得:x2+x-1≤kx,这里要求k的范围,因为x>0,所以不等式两边可同除以x,得到k≥x-
+1,所以这里只要让k大于等于x-
+1的最大值,所以转而求函数x-
+1的最大值即可.
(2)要证明函数f(x)在(
,1)内存在零点,则一定有f(
) 和f(1) 异号,光是异号还不行,一般的需要f(x)在(
,1)上单调.这些条件都找到了,这道题的答案也就接出来了.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
(2)要证明函数f(x)在(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)n=2时,f(x)=x2+x-1,所以由f(x)≤kx得:x2+x-1≤kx;
∵x>0∴k≥x-
+1;
令g(x)=x-
+1,则g′(x)=
+1>0,所以g(x)在(0,1]上是增函数,g(x)max=g(1)=1;
所以k≥1.
(2)f′(x)=xn-1+xn-2+…+1=
,且在(
,1)上,0<xn<1,1-xn>0,1-x>0,所以在(
,1)上f′(x)>0;
所以f(x)在(
,1)上是增函数,且f(1)=n-1>0,f(
)=(
)n+(
)n-1+…+
-1=
-1=-(
)n<0;
所以f(x)在(
,1)内存在唯一的零点.
∵x>0∴k≥x-
| 1 |
| x |
令g(x)=x-
| 1 |
| x |
| 1 |
| x2 |
所以k≥1.
(2)f′(x)=xn-1+xn-2+…+1=
| 1-xn |
| 1-x |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)在(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
所以f(x)在(
| 1 |
| 2 |
点评:需注意的,或解这道题的关键点就是在所得不等式两边同除x,而第二问所用的是证明一般函数在某个区间上有零点基本方法,须记住并理解.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的(1)、(2)、(3)、(4).则图中的甲、乙的运算式可以表示为:( )
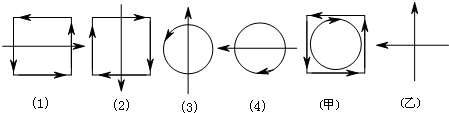

| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |
 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)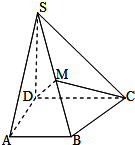 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.