题目内容
1.已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)=2g(x)+$\frac{x-4}{{x}^{2}+1}$,则下列结论中正确的序号是①④①f($\frac{1}{x}$)=f(x);
②f(x)在($\frac{1}{2}$,+∞)上单调递减;
③g(x)在(0,+∞)上单调递增;
④若f($\frac{1}{{x}^{2}+1}$)+f(4x-4x2-2)≥0,则x∈(-∞,$\frac{1}{3}$]∪[1,+∞)
分析 求出函数的解析式,再进行验证,即可得出结论.
解答 解:由题意,-f(x)=2g(x)+$\frac{-x-4}{{x}^{2}+1}$,∴f(x)=$\frac{2x}{{x}^{2}+1}$,g(x)=$\frac{2}{{x}^{2}+1}$;
①f($\frac{1}{x}$)=$\frac{\frac{2}{x}}{\frac{1}{{x}^{2}}+1}$=$\frac{2x}{{x}^{2}+1}$=f(x),正确;
②∵f(x)=$\frac{2x}{{x}^{2}+1}$,∴f′(x)=$\frac{2(1-{x}^{2})}{({x}^{2}+1)^{2}}$,f(x)在(1,+∞)上单调递减,不正确;
③g′(x)=$\frac{-4x}{({x}^{2}+1)^{2}}$,∴g(x)在(0,+∞)上单调递减,不正确;
④利用①f($\frac{1}{x}$)=$\frac{\frac{2}{x}}{\frac{1}{{x}^{2}}+1}$=$\frac{2x}{{x}^{2}+1}$=f(x),知f($\frac{1}{{x}^{2}+1}$)=f(x2+1),故f($\frac{1}{{x}^{2}+1}$)+f(4x-4x2-2)≥0?f(x2+1)≥f(4x2-4x+2)=f((2x-1)2+1),再利用f(x)在(1,+∞)上单调递减,得x2+1≤-4x+4x2+2,∴3x2-4x+1≥0,∴x∈(-∞,$\frac{1}{3}$]∪[1,+∞),正确.
故答案为①④.
点评 本题考查函数的单调性与奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.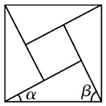 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | 0 |
8.若数列{an}的前n项和为Sn,S2n-12+S2n2=4(a2n-2),则2a1+a100=( )
| A. | -8 | B. | -6 | C. | 0 | D. | 2 |
6.四面体A-BCD中,AB=CD=10,AC=BD=2$\sqrt{34}$,AD=BC=2$\sqrt{41}$,则四面体A-BCD外接球的表面积为( )
| A. | 50π | B. | 100π | C. | 200π | D. | 300π |
10.已知数据x,y的取值如表:
从散点图可知,y与x呈线性相关关系,已知第四组数据在回归直线$\hat y=0.8x+\hat a$上,则m的取值为13.8.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
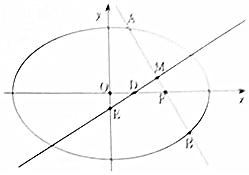 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.