题目内容
6.已知函数f(x)=2cos2x+$\sqrt{3}$sin2x-1.(1)求f($\frac{π}{6}$)的值;
(2)求函数f(x)的最小正周期和单调递增区间.
分析 (1)直接代入计算;(2)利用二倍角公式与和差公式对f(x)进行化简,结合正弦函数的单调性列出不等式解出.
解答 解:(1)f($\frac{π}{6}$)=2cos2($\frac{π}{6}$)+$\sqrt{3}$sin$\frac{π}{3}$-1=2×($\frac{\sqrt{3}}{2}$)2+$\sqrt{3}$×$\frac{\sqrt{3}}{2}$-1=2.
(2)f(x)=cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$).
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π.
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ.解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ.
∴f(x)的单调增区间是[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z.
点评 本题考查了三角函数的化简求值与性质.是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列函数中,既是偶函数,周期为π的是( )
| A. | y=sin|x| | B. | y=|tanx| | C. | y=|sin2x| | D. | y=cos(2x+$\frac{x}{2}$) |
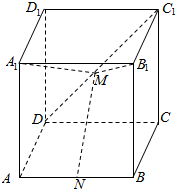 如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.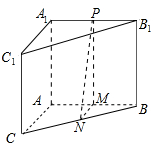 在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.
在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.