题目内容
20.设函数$f(x)=sin(2x-\frac{π}{6})$,则该函数的最小正周期为π,f(x)在$[0,\frac{π}{2}]$的最小值为-$\frac{1}{2}$.分析 由条件利用正弦函数的周期性求得函数的最小正周期,再利用正弦函数的定义域和值域,求得它的最小值.
解答 解:根据函数$f(x)=sin(2x-\frac{π}{6})$,可得则该函数的最小正周期为$\frac{2π}{2}$=π,
当x∈[0,$\frac{π}{2}$]时,2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],故当2x-$\frac{π}{6}$=-$\frac{π}{6}$ 时,f(x)取得最小值为-$\frac{1}{2}$,
故答案为:π,$-\frac{1}{2}$.
点评 本题主要考查正弦函数的周期性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.等比数列{an}中,a3a5=64,则a4=( )
| A. | 8 | B. | -8 | C. | 8或-8 | D. | 16 |
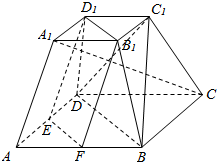 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.