题目内容
已知抛物线C1:y2=4x和C2:x2=2py(p>0)的焦点分别为F1,F2,C1,C2交于O,A两点(O为坐标原点),且F1F2⊥OA.
(1)求抛物线C2的方程;
(2)过点O的直线交C1的下半部分于点M,交C2的左半部分于点N,点P坐标为(-1,-1),求△PMN面积的最小值.
(1)求抛物线C2的方程;
(2)过点O的直线交C1的下半部分于点M,交C2的左半部分于点N,点P坐标为(-1,-1),求△PMN面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=(-1,
),联立
,解得
,或
,得到
=(
,
),由此能求出C2的方程.
(2)设过O的直线方程为y=kx,联立
,得M(
,
),联立
,得N(4k,4k2),由此利用点到直线的距离公式能求出△PMN面积取得最小值.
| F1F2 |
| p |
| 2 |
|
|
|
| OA |
| 3 | 16p2 |
| 3 | 32p |
(2)设过O的直线方程为y=kx,联立
|
| 4 |
| k2 |
| 4 |
| k |
|
解答:
解:(1)由已知得:F1(1,0),F2(0,
),∴
=(-1,
),…(1分)
联立
,解得
,或
,
即O(0,0),A(
,
),
∴
=(
,
),…(3分)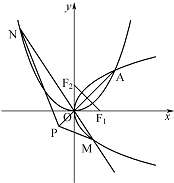
∵F1F2⊥OA,∴
•
=0,
即-
+
=0,解得p=2,∴C2的方程为x2=4y.…(5分)
(2)设过O的直线方程为y=kx,(k<0),
联立
,得M(
,
),联立
,得N(4k,4k2),…(7分)
P(-1,-1)在直线y=x上,设点M到直线y=x的距离为d1,点N到直线y=x的距离为d2,
则S△PMN=
•|OP|•(|d1|+|d2|)…(8分)
=
×
×(
+
)
=2(|
-
|+|k-k2|)
=2(-
-k+
+k2)…(10分)
≥2(2
+2
)=8,
当且仅当k=-1时,“=”成立,即当过原点直线为y=-x时,…(11分)
△PMN面积取得最小值8.…(12分)
| p |
| 2 |
| F1F2 |
| p |
| 2 |
联立
|
|
|
即O(0,0),A(
| 3 | 16p2 |
| 3 | 32p |
∴
| OA |
| 3 | 16p2 |
| 3 | 32p |

∵F1F2⊥OA,∴
| F1F2 |
| OA |
即-
| 3 | 16p2 |
| p |
| 2 |
| 3 | 32p |
(2)设过O的直线方程为y=kx,(k<0),
联立
|
| 4 |
| k2 |
| 4 |
| k |
|
P(-1,-1)在直线y=x上,设点M到直线y=x的距离为d1,点N到直线y=x的距离为d2,
则S△PMN=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
|
| ||||
|
| |4k-4k2| | ||
|
=2(|
| 1 |
| k |
| 1 |
| k2 |
=2(-
| 1 |
| k |
| 1 |
| k2 |
≥2(2
(-
|
|
当且仅当k=-1时,“=”成立,即当过原点直线为y=-x时,…(11分)
△PMN面积取得最小值8.…(12分)
点评:本题考查抛物线方程的求法,考查三角形面积的最小值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
 如图所示,某地有一段网格状公路,小王开车从A处出发,选择最近的路线去往B处.因道路检修,虚线处公路无法行驶.若行至S路口处,小王会随机选择开向C,D两个路口之一,再选择避开S的最近路线继续行至B处,则小王共有( )种不同的行驶路线.
如图所示,某地有一段网格状公路,小王开车从A处出发,选择最近的路线去往B处.因道路检修,虚线处公路无法行驶.若行至S路口处,小王会随机选择开向C,D两个路口之一,再选择避开S的最近路线继续行至B处,则小王共有( )种不同的行驶路线.
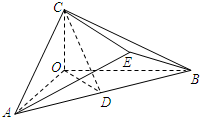 如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2
如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2