题目内容
下列命题:
①已知ab≠0,若a-b=1,则a3-b3-ab-a2-b2=0;
②若函数f(x)=(x-a)(x+2)为偶函数,则实数a的值为-2;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则k=2;
④若tanθ=2,则cos2θ=-
.
其中真命题是 (填上所有真命题的序号)
①已知ab≠0,若a-b=1,则a3-b3-ab-a2-b2=0;
②若函数f(x)=(x-a)(x+2)为偶函数,则实数a的值为-2;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则k=2;
④若tanθ=2,则cos2θ=-
| 3 |
| 5 |
其中真命题是
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①先将a3-b3-ab-a2-b2因式分解:a3-b3-ab-a2-b2=(a-b-1)(a2+ab+b2),利用a-b=1即可得出结论;
②运用函数的奇偶性的定义,将x换成-x,注意变形,运用恒等知识得到对应项系数相等;
③圆心(1,0)在直线上,代入可求;
④tanθ=2,利用cos2θ=
可求.
②运用函数的奇偶性的定义,将x换成-x,注意变形,运用恒等知识得到对应项系数相等;
③圆心(1,0)在直线上,代入可求;
④tanθ=2,利用cos2θ=
| 1-tan2θ |
| 1+tan2θ |
解答:
解:①由于a3-b3-ab-a2-b2=(a-b-1)(a2+ab+b2),∵a-b=1,∴a-b-1,∴a3-b3-ab-a2-b2=(a-b-1)(a2+ab+b2)=0,正确;
②∵函数f(x)=(x+2)(x-a)是偶函数,∴f(-x)=f(x),即x2+(a-2)x-2a=x2+(2-a)x-2a,
∴a-2=2-a,∴a=2,故不正确;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则圆心(1,0)在直线上,∴k=-2,故不正确;
④若tanθ=2,则cos2θ=
=
=-
,正确.
故答案为:①④.
②∵函数f(x)=(x+2)(x-a)是偶函数,∴f(-x)=f(x),即x2+(a-2)x-2a=x2+(2-a)x-2a,
∴a-2=2-a,∴a=2,故不正确;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则圆心(1,0)在直线上,∴k=-2,故不正确;
④若tanθ=2,则cos2θ=
| 1-tan2θ |
| 1+tan2θ |
| 1-4 |
| 1+4 |
| 3 |
| 5 |
故答案为:①④.
点评:本题考查命题的真假判断与应用,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
相关题目
已知i为虚数单位,若1-bi=
,则a+bi的模等于( )
| 2i |
| a+i |
A、
| ||
| B、2 | ||
| C、4 | ||
| D、1 |

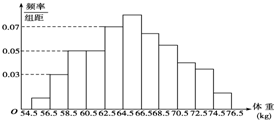 为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是
为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是