题目内容
过抛物线y2=4x（p＞0）的焦点作两条互相垂直的弦AB、CD，则
+
=（ ）
| 1 |
| |AB| |
| 1 |
| |CD| |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
考点：直线与圆锥曲线的关系,抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设出两直线的倾斜角，利用焦点弦的弦长公式分别表示出|AB|，|CD|即可求得答案．
解答：
解：抛物线y2=4x，可知2p=4，
设直线l1的倾斜角为θ，则l2的倾斜角为
-θ，
过焦点的弦，|AB|=
，|CD|=
=
∴
+
=
+
=
=
，
故选D．
设直线l1的倾斜角为θ，则l2的倾斜角为
| π |
| 2 |
过焦点的弦，|AB|=
| 2p |
| sin2θ |
| 2p | ||
sin2(
|
| 2p |
| cos2θ |
∴
| 1 |
| |AB| |
| 1 |
| |CD| |
| sin2θ |
| 2p |
| cos2θ |
| 2p |
| 1 |
| 2p |
| 1 |
| 4 |
故选D．
点评：本题主要考查了抛物线的简单性质．对于过焦点的弦，能熟练掌握相关的结论，解决问题事半功倍．
练习册系列答案
相关题目
下列各组角中终边相同的角是（ ）
A、
| ||||
B、kπ±
| ||||
| C、（2k+1）π与（4k±π）（k∈Z） | ||||
D、kπ+
|
已知集合A={x|x2-2x≤0，x∈R}，集合B={x||x|≤1，x∈R}，则A∩B为（ ）
| A、{x|0≤x≤2} |
| B、{x|1≤x≤2} |
| C、{x|-1≤x≤2} |
| D、{x|0≤x≤1} |
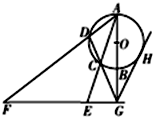如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点G作 AB的垂线，交AC的延长线于点 E，交AD的延长线于点F，过G作⊙O的切线，切点为H，求证：
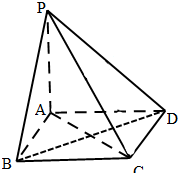已知四棱锥P-ABCD中，PA⊥面ABCD，四边形ABCD是正方形，且AB=a，PA=
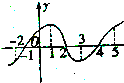如图所示的是函数y=f（x）的导函数y=f′（x）的图象，则[-2，5]上函数f（x）的递增区间为
如图，已知圆O：x2+y2=64分别与x轴、y轴的正半轴交于点A、B，直线l：y=kx-k+2分别于x轴、y轴的正半轴交于点N、M．