题目内容
已知各顶点都在一个球面上的正方体的棱长为2,则这个球的体积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求出正方体的对角线的长度,就是外接球的直径,利用球的体积公式求解即可.
解答:
解:因为一个正方体的顶点都在球面上,它的棱长为2,
所以正方体的外接球的直径就是正方体的对角线的长度:2
.
所以球的半径为:
.
所求球的体积为:
×(
)3=4
π.
故答案为:4
π.
所以正方体的外接球的直径就是正方体的对角线的长度:2
| 3 |
所以球的半径为:
| 3 |
所求球的体积为:
| 4π |
| 3 |
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题考查球的内接体,球的体积的求法,求出球的半径是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知a,b,c,d均为实数,下列命题中正确的是( )
| A、a>b⇒ac2>bc2 |
| B、a<b<0,c<d<0⇒ac<bd |
| C、a>b,ac<bc⇒c>0 |
| D、a>b,c>d⇒a+c>b+d |
若x>0,y>0,则“x2+y2>1”是“x+y>1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
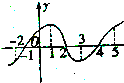 如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为
如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为 如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.
如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.